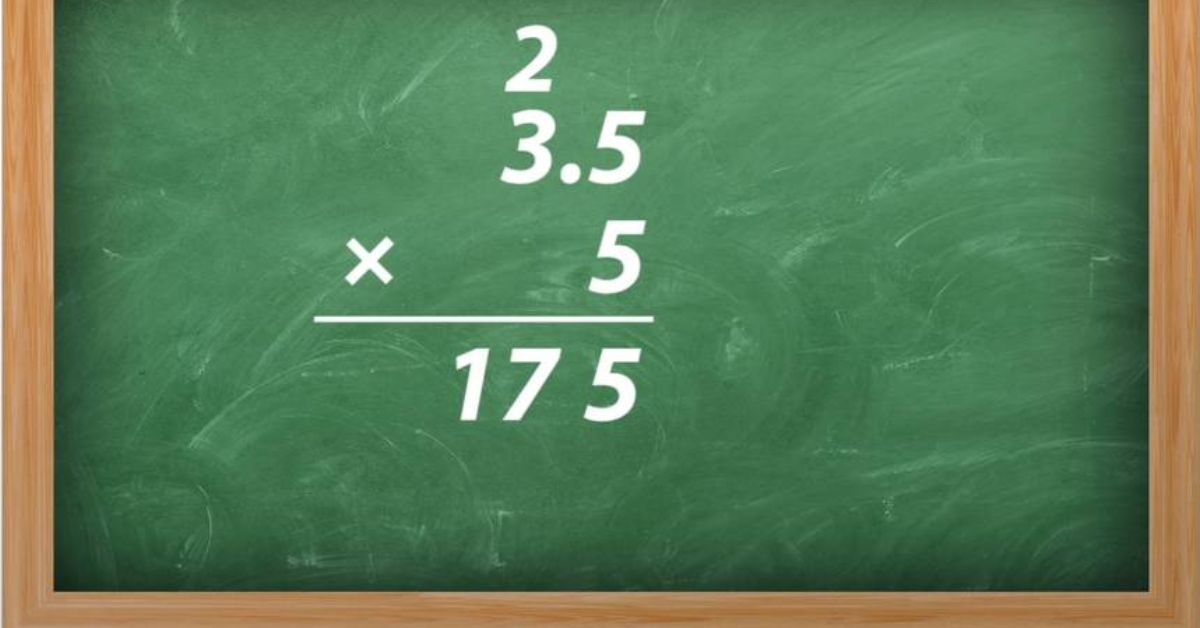Decimal numbers are a basic concept in mathematics, playing an important role in representing and performing operations with non-integer values. In today’s article, let’s learn about the definitions related to this type of number as well as practice math problems to further consolidate our mathematical knowledge.
What is a decimal fraction?
Types of exercises
Decimal number problems require a solid understanding of how the number system works and skills in performing the associated operations. In this group of problems, we will focus on the basic aspects of decimal numbers, including how decimal numbers are represented, addition, subtraction, multiplication, division, and issues related to conversion between decimal numbers and different number systems.
Bạn đang xem: Số thập phân là gì? Phân số thập phân là gì? Các phép tính với số thập phân
Form 1: Reading decimal fractions
Exercise: Read the following decimal fractions:
a) October 25
b) 75/100
c) 6/10
d) 125/1000
e) 3/100
f) October 23
g) 45/1000
h) 10/33

The answer:
a) 25/10 is read as “twenty-five tenths”
b) 75/100 is read as “seventy-five one hundredths”
c) 6/10 is read as “six tenths”
d) 125/1000 is read as “one hundred twenty-five thousandths”
e) 3/100 is read as “three parts one hundred”
f) 23/10 is read as “twenty-three tenths”
g) 45/1000 is read as “forty-five thousandths”
h) 33/10 is read as “thirty-three tenths”
Form 2: Write decimal fractions
Exercise 1: Write the following decimal fractions as fractions:
a) 0.4
b) 0.9
c) 0.125
d) 0.75
The answer:
a) 0.4 written as a fraction is 4/10
b) 0.9 written as a fraction is 9/10
c) 0.125 written as a fraction is 125/1000
d) 0.75 written as a fraction is 75/100
Exercise 2: Write the following decimal fractions:
a) Thirty-two one-hundredths
b) Five thousandths
c) Seventy-two ten-thousandths
d) Eight-tenths
The answer:
a) Thirty-two hundredths: 32/100
b) Five thousandths: 5/1000
c) Seventy-two ten-thousandths: 72/10000
d) Eight-tenths: 8/10
Form 3: Write fractions as decimal fractions
Exercise: Write the following fractions as decimal fractions:
a) 3/5
b) 1/2
c) 7/8
d) 2/3

The answer:
a) 3/5 = 0.6 = 6/10
b) 1/2 = 0.5 = 5/10
c) 7/8 = 0.875 = 875/1000
d) 2/3 = 0.66666 (or round to 0.67) = 67/100
Form 4: Compare two decimal fractions
Exercise: Compare the following two decimal numbers:
a) 0.25 and 0.3
b) 0.8 and 0.75
c) 0.125 and 0.15
Xem thêm : Bảng tra cứu biển số xe các tỉnh
d) 0.5 and 0.5

The answer:
a) 0.25 and 0.3
First convert to fractions with the same denominator, we get 25/100 and 30/100. Compare the numerators, we get 25 < 30
Conclusion: 0.25 < 0.3
b) 0.8 and 0.75
First convert to fractions with the same denominator, we get 80/100 and 75/100. Compare the numerators, we get 80 > 75
Conclusion: 0.8 > 0.75
c) 0.125 and 0.15
First convert to fractions with the same denominator, we get 125/1000 and 150/1000. Compare the numerators, we get 125 < 150
Conclusion: 0.125 < 0.15
Xem thêm : Bảng tra cứu biển số xe các tỉnh
d) 0.5 and 0.5
First convert to fractions with the same denominator, we get 5/10 and 5/10. Compare the numerators, we get 5 = 5
Conclusion: 0.5 = 0.5
Form 5: Addition and subtraction of decimal fractions
Exercise 1: Calculate the sum of the following decimal fractions:
a) 0.25 + 0.4
b) 0.8 + 0.35
c) 0.125 + 0.05
d) 0.6 + 0.75
e) 0.1 + 0.2
f) 0.35 + 0.45
g) 0.6 + 0.15
h) 0.9 + 0.05
Instructions: To add decimal numbers together, we take the integer part and add the integer part, then add the decimal part to the decimal part.
The answer:
a) 0.25 + 0.4 = 0.65
b) 0.8 + 0.35 = 1.15
c) 0.125 + 0.05 = 0.175
d) 0.6 + 0.75 = 1.35
e) 0.1 + 0.2 = 0.3
f) 0.35 + 0.45 = 0.8
g) 0.6 + 0.15 = 0.75
h) 0.9 + 0.05 = 0.95

Exercise 2: Calculate the difference of the following decimal fractions:
a) 0.6 – 0.25
b) 0.8 – 0.35
c) 0.125 – 0.05
d) 0.9 – 0.75
e) 0.4 – 0.2
f) 0.35 – 0.15
g) 0.6 – 0.3
h) 0.9 – 0.05
Instructions: Do the same as adding decimal numbers, subtract the integer part from the integer part and subtract the decimal part from the decimal part.
The answer:
a) 0.6 – 0.25 = 0.35
b) 0.8 – 0.35 = 0.45
c) 0.125 – 0.05 = 0.075
d) 0.9 – 0.75 = 0.15
e) 0.4 – 0.2 = 0.2
f) 0.35 – 0.15 = 0.2
g) 0.6 – 0.3 = 0.3
h) 0.9 – 0.05 = 0.85
Form 6: Multiplication of decimal fractions
Multiply a decimal number by a decimal number
Steps to follow: To multiply two decimal numbers together, we can apply the following steps:
Step 1: We start by setting up the calculation as usual, with the first decimal number being the units place and the second decimal number being the tens place or any other place depending on the number of decimal places each number has.
Xem thêm : Lệ phí trước bạ là gì? Quy định cách tính và mức thu lệ phí trước bạ
Step 2: After setting up the calculation, we perform the multiplication as we would multiply two normal natural numbers. To do this, we multiply each digit of the first number by each digit of the second number, starting from right to left. When multiplying, we should note that the decimal places of the product will be determined later.
Step 3: After performing the multiplication, we will have a sum of the products of the digits. To determine the position of the decimal point in the result, we use the number of decimal places of each factor. The position of the decimal point in the result will be at the exact position where the total number of decimal places of both factors is known from right to left.

Through the above three steps, we can multiply two decimal numbers together accurately. However, when performing this process, we need to pay attention and make sure that we have placed the decimal point correctly and calculated the decimal part of the result correctly.
Example problem: 3.4 x 1.2
3.4
x
1.2
—-
68
+
34
—-
4.08
So: 3.4 x 1.2 = 4.08

Multiply a decimal number by 0.1; 0.01; 0.001; 0.0001
When multiplying any decimal number by the following numbers 0.1; 0.01; 0.001; 0.0001;… we can apply the simple rule of moving the decimal point of the original decimal number to the left, corresponding to the number of digits after the decimal point of that number. To do this, we will consider the decimal number and determine the number of decimal places in it. Then, we move the decimal point to the left one, two, three, four,… digits corresponding to the number of decimal places in that number.
For example 1, if we have the decimal number 2.345 and want to multiply it by 0.01, we see that this number 0.01 has two decimal places. Therefore, we will move the decimal point of the number 2.345 two places to the left, and the result will be 0.02345.
Example 2, similarly, if we have the decimal number 7.89 and we want to multiply it by 0.001, we see that this number 0.001 has three decimal places. So we will move the decimal point three places to the left, and the result will be 0.00789.

This rule helps us simplify the process of multiplying decimal numbers by numbers such as 0.1; 0.01; 0.001; 0.0001;…, saving time and also minimizing errors during calculation.
Multiply a decimal by a natural number
Steps to follow: When you want to multiply a decimal number by a natural number, you can apply the following rule:
Step 1: We start by multiplying the digits of the natural number by each digit of the decimal number, starting from right to left. Similar to the normal multiplication rule, we multiply each pair of digits and record the temporary result.
Step 2: After performing the multiplication, we look at the decimal part of the decimal number and count the number of digits in that part. This number of digits will determine the position of the decimal point in the result. We will place commas separating the digits in the product, starting from right to left, corresponding to the number of digits in the decimal part.
Example problem: 3.18 x 4
3.18
x
4
——
12.72
So: 3.18 x 4 = 12.72

Multiply a decimal number by 10, 100, 1000,…
When we want to multiply any decimal number by 10, 100, 1000, … we can apply the simple rule of moving the decimal point of that number to the right by one, two, three, … digits. To do this, we just need to consider the decimal number and determine the number of decimal places in it. Next, we will move the decimal point to the right by the number of digits corresponding to the number of decimal places in that number.
For example 1, if we have the decimal number 2.345 and want to multiply it by 10, we see that the number 10 has a leading zero. To multiply by 10, we just need to move the decimal point one place to the right, and the result will be 23.45.
Example 2, similarly, if we have the decimal number 7.89 and want to multiply it by 100, we see that the number 100 has two zeros. So we will move the decimal point two places to the right, and the result will be 789.

This rule helps us get the result of multiplying a decimal number by 10, 100, 1000, … quickly. Just move the decimal point to the right a number of digits corresponding to the number of decimal digits of the original decimal number. This helps us save time and minimize errors in the calculation process.
Form 7: Division of decimal fractions
Divide a decimal number by a decimal number
Steps to follow: When you want to divide a decimal number by a decimal number, you can apply the following rule:
Step 1: We look at the divisor and count the number of digits in its decimal part. This number of digits will determine the number of decimal places in the result.
Step 2: After determining the number of decimal places of the divisor, we will move the decimal point of the dividend to the right by the corresponding number of digits. This is equivalent to removing the decimal point of the dividend.
Step 3: After removing the decimal point of the dividend, we divide as we would with a natural number. We perform the division and record the temporary result.
Example problem: Example: 13.11 : 2.3

- We have the decimal part of the number 2.3 with one digit
- Move the decimal point of the number 13,11 to the right one digit to get 131,1 and remove one decimal point from the number 2,3 to get 23.
- Then we divide 131.1 : 23 as usual.
Divide a decimal by a natural number
Steps to follow: When you want to divide a decimal number by a natural number, you can apply the following rule:
Step 1: We start by taking the integer part of the dividend and dividing it by the divisor as usual when dividing a natural number. The result of this division will be the integer part of the final result.
Step 2: After having the integer part of the result, we write a decimal point to the right of the quotient we found. Next, we take the first digit in the decimal part of the dividend and put it behind the decimal point. We will use this digit to continue dividing.
Step 3: After having the first digit in the decimal part of the dividend, we continue to divide each subsequent digit in the decimal part. We take each of these digits and perform the division as we would divide a natural number. The result of each division will be the next digits of the final result.
Example problem: 37.52 : 4

- Divide the integer part 37 by 4 to get 9 as the integer part of the result and remainder 1.
- Write a comma to the right of the found quotient, we have 9
- The next number after the decimal point is 5, we have 15 divided by 4 gets 3 remainder 3
- Lower the next number of the dividend to 2, we get 32 divided by 4, we get 8, remainder 0.
- Combining the results from the above divisions, the final result is 9.38
Divide a natural number by a decimal number
Steps to follow: When you want to divide a natural number by a decimal number, you can apply the following rule:
Step 1: We look at the divisor and count the number of digits in its decimal part. This number of digits will determine the number of decimal places in the result.
Step 2: After determining the number of decimal places of the divisor, we add that many zeros to the right of the dividend. This is equivalent to removing the decimal point of the divisor.
Step 3: After removing the decimal point of the divisor, we divide as we do with natural numbers. We divide and record the temporary result.
Example problem: 4:1.25

- We see that the decimal part of the number 1.25 has two digits.
- Add two more zeros to the right of the number 4 to get the dividend 400 and remove the decimal point from the divisor to get the number 125.
- Then we divide as usual and get the result of 3.2.
Conclusion
In this article of Hoang Ha Mobile, that with the close relationship between decimals and other types of numbers, we have a solid foundation to grasp more complex mathematical concepts. The calculation problem that we have compiled in this article is not only an important part of the curriculum but also an important skill that helps us better understand the world around us and master different aspects of life related to measurement and calculation.
SEE MORE:
Nguồn: https://tuyengiaothudo.vn
Danh mục: Hỏi Đáp