Trung vị là một khái niệm phổ biến trong hình học không gian và chủ yếu được áp dụng trong hình tam giác. Với kiến thức về khái niệm và công thức tính toán, chúng ta có thể áp dụng chúng để giải các bài toán hình học liên quan đến hình tam giác một cách dễ dàng. Trong bài viết này, chúng ta hãy cùng tìm hiểu trung vị là gì và một số bài tập để làm quen với chủ đề này.
Đường trung tuyến là gì?
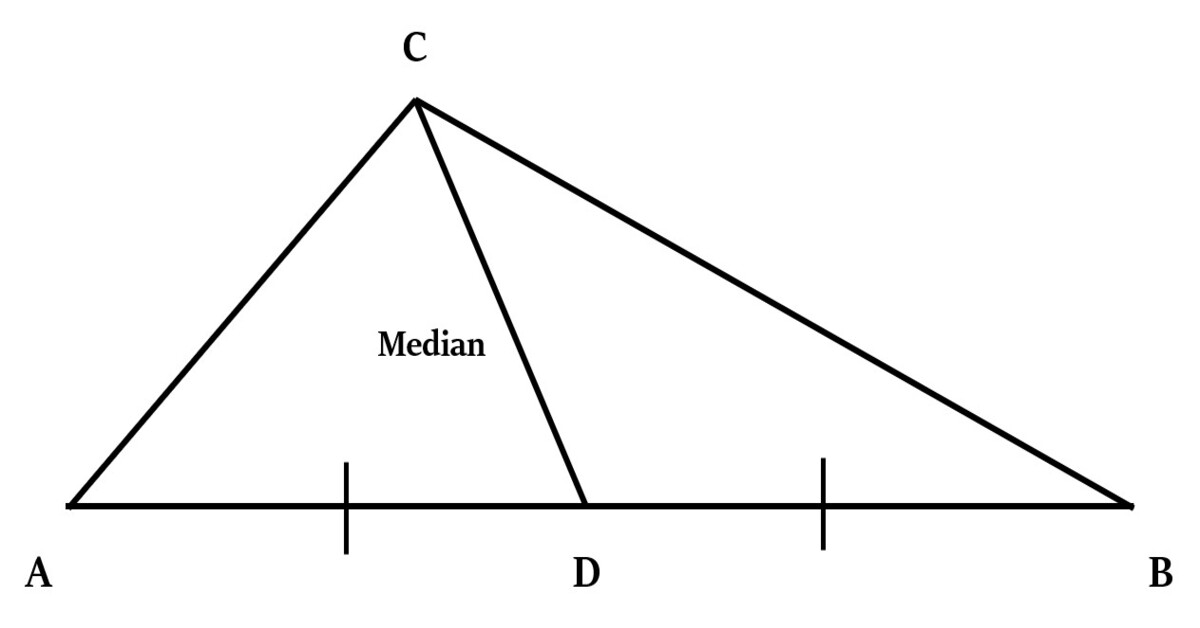
Đường trung tuyến là bất kỳ đường thẳng nào đi qua trung điểm của một đoạn thẳng. Trong một tam giác, đường trung tuyến là một đoạn thẳng nối một đỉnh của tam giác với trung điểm của cạnh đối diện của tam giác. Mỗi tam giác có ba đường trung tuyến, và ba đường trung tuyến này cắt nhau tại một điểm gọi là tâm của tam giác. Tâm của một tam giác có một số tính chất đặc biệt, chẳng hạn như bằng hai phần ba khoảng cách từ mỗi đỉnh đến đường trung tuyến tương ứng với đỉnh đó.
Bạn đang xem: Đường trung tuyến là gì? Tính chất, công thức và bài tập tính đường trung tuyến

Một tính chất quan trọng khác của đường trung tuyến là nó chia diện tích của tam giác thành hai phần bằng nhau. Ngoài ra, ba đường trung tuyến chia tam giác thành sáu tam giác nhỏ hơn có diện tích bằng nhau. Điều này có thể được chứng minh bằng định lý Apollonius hoặc bằng cách sử dụng các công thức tính diện tích tam giác.
Đường trung tuyến cũng có một số đặc điểm riêng trong các tam giác đặc biệt như tam giác vuông, tam giác cân hoặc tam giác đều. Ví dụ, trong tam giác vuông, đường trung tuyến tương ứng với cạnh huyền bằng một nửa độ dài cạnh huyền. Trong tam giác cân, đường trung tuyến tương ứng với đáy vuông góc với đáy và chia tam giác thành hai tam giác bằng nhau. Trong tam giác đều, mỗi đường trung tuyến cũng là đường cao, đường phân giác và đường phân giác vuông góc của tam giác.
Đường trung tuyến có đặc điểm gì?
Tính chất của đường trung tuyến là một trong những khía cạnh quan trọng của hình học tam giác. Bằng cách khám phá tính chất của đường trung tuyến, chúng ta có thể hiểu sâu hơn về cấu trúc và mối quan hệ trong một tam giác. Đường trung tuyến có một số tính chất đặc biệt trong các loại tam giác khác nhau. Sau đây là một số thông tin cụ thể về tính chất của đường thẳng này:
Trong tam giác cân, đường trung tuyến ứng với đáy vuông góc với đáy và chia tam giác thành hai tam giác bằng nhau. Trong tam giác đều, ba đường trung tuyến vuông góc với các cạnh đối diện và chia tam giác thành sáu tam giác đều nhỏ hơn.

Trong một tam giác vuông, đường trung tuyến dọc theo cạnh huyền bằng một nửa độ dài cạnh huyền và chia tam giác thành hai tam giác giống với tam giác ban đầu. Đường trung tuyến dọc theo một cạnh bằng trung bình cộng của độ dài cạnh huyền và độ dài cạnh đối diện.
Đối với các tam giác đồng dạng, tỉ số độ dài các đường trung tuyến ứng với các cạnh đối diện sẽ bằng tỉ số độ dài các cạnh tương ứng của hai tam giác. Nghĩa là, nếu tam giác ABC đồng dạng với tam giác A’B’C’ thì AD/BC = A’D’/B’C’.
Định lý trung tuyến trong hình học
Sau khi tìm hiểu thêm về trung vị là gì, chúng ta có thể thấy rằng đoạn thẳng này đóng vai trò quan trọng trong nghiên cứu về tam giác và có một số định lý liên quan đến nó. Mỗi định lý có thể được áp dụng trong nhiều trường hợp khác nhau. Dưới đây là ba định lý cơ bản về trung vị trong tam giác.
Hai đường trung tuyến trong một tam giác chia đôi chiều dài của chúng.
Định lý này phát biểu rằng hai đường trung tuyến của một tam giác chia nhau thành hai phần bằng nhau. Điều này có nghĩa là đường trung tuyến từ một đỉnh của tam giác đến trung điểm của cạnh đối diện bằng một nửa độ dài của đường trung tuyến từ đỉnh kia đến trung điểm của cạnh đối diện. Định lý trên đưa ra một bài toán thú vị về mối quan hệ giữa các đường trung tuyến và các cạnh của một tam giác.

Để hiểu rõ hơn về định lý này, hãy xem xét bất kỳ tam giác nào. Giả sử chúng ta có bất kỳ tam giác ABC nào. Đường trung tuyến từ đỉnh A đến trung điểm BC sẽ bằng một nửa độ dài đường trung tuyến từ đỉnh B đến trung điểm AC. Tương tự, đường trung tuyến từ đỉnh A đến trung điểm AC sẽ bằng một nửa độ dài đường trung tuyến từ đỉnh C đến trung điểm AB. Điều này ngụ ý rằng hai đường trung tuyến này sẽ chia hết chiều dài cho nhau.
Đường trung tuyến và cạnh tương ứng của tam giác tạo thành một đoạn thẳng song song.
Định lý này được xác định bằng cách định nghĩa trung tuyến là gì và các tính chất của nó trong một tam giác. Từ đó, chúng ta biết rằng đoạn thẳng này và cạnh tương ứng của tam giác là hai đường thẳng song song. Do đó, trung tuyến từ một đỉnh của một tam giác đến điểm giữa của cạnh đối diện thì song song với cạnh tương ứng. Định lý này cho thấy một tính chất quan trọng của trung tuyến và mối quan hệ của nó với các cạnh của một tam giác.

Để hiểu rõ hơn, hãy xét tam giác ABC và đường trung tuyến AH từ đỉnh A đến trung điểm M của cạnh BC. Đường trung tuyến AH và cạnh BC tương ứng tạo thành một đường thẳng duy nhất và Định lý 2 khẳng định rằng đường thẳng này là một đoạn thẳng song song.
Ba đường trung tuyến của một tam giác cắt nhau tại một điểm.
Xem thêm : Đầu số 037 là mạng gì? Ý nghĩa của đầu số là gì?
Ba đường trung tuyến của một tam giác cắt nhau tại một điểm duy nhất, đó là trọng tâm của tam giác. Trọng tâm được định nghĩa là trung điểm của các đoạn thẳng nối các đỉnh của tam giác với trung điểm của các cạnh đối diện. Đây là một điểm đặc biệt trong tam giác vì nó có một số tính chất đáng chú ý.

Tâm có một tính chất độc đáo là tổng các vectơ từ tâm đến các đỉnh của tam giác bằng không. Điều này có nghĩa là nếu chúng ta vẽ các vectơ từ tâm đến các đỉnh và cộng chúng lại, tổng kết quả sẽ bằng không. Điều này cho thấy tam giác cân bằng và cho thấy tâm nằm ở tâm hình học của tam giác.
Ngoài ra, tâm là đặc biệt vì nó chia ba đường trung tuyến theo tỷ lệ 1:2. Điều này có nghĩa là đường trung tuyến từ tâm đến bất kỳ đỉnh nào sẽ dài gấp đôi đường trung tuyến từ tâm đến điểm giữa của cạnh đối diện. Tỷ lệ này biểu thị mối quan hệ đặc biệt giữa tâm và các đường trung tuyến, tạo ra sự phân bố đều và cân bằng trong tam giác.
Công thức tính đường trung tuyến là gì?
Để tính trung vị của một tam giác, chúng ta cần biết một số thông tin cơ bản về tam giác, bao gồm độ dài các cạnh và tọa độ các đỉnh của tam giác. Công thức tính trung vị phụ thuộc vào thông tin này và có thể áp dụng dễ dàng.
Công thức tính tọa độ trung điểm của cạnh BC
Giả sử ta có tam giác ABC với tọa độ các đỉnh A(x1, y1), B(x2, y2), C(x3, y3). Để tính tọa độ điểm D là trung điểm của cạnh BC, ta có thể sử dụng công thức sau:
Tọa độ x của D bằng trung bình cộng của tọa độ x của B và C, tức là: xD = (x2 + x3) / 2.
Tọa độ y của D bằng trung bình cộng của tọa độ y của B và C, tức là: yD = (y2 + y3) / 2.

Với x là tọa độ x của trung điểm cạnh BC và y là tung độ của trung điểm cạnh BC. Vì vậy, bây giờ tọa độ của D sẽ được xác định là D((x2 + x3) / 2, (y2 + y3) / 2).
Công thức tính tọa độ trung điểm các cạnh còn lại
Tương tự như trên, dựa trên định nghĩa về trung vị và một số thông tin khác, chúng ta có thể tính tọa độ của các điểm E và F là trung điểm của các cạnh AC và AB bằng cách sử dụng công thức sau:
Tọa độ x của E bằng trung bình cộng của tọa độ x của A và C, tức là: xE = (x1 + x3) / 2.
Tọa độ y của E bằng trung bình cộng của tọa độ y của A và C, tức là: yE = (y1 + y3) / 2.

Tọa độ x của F bằng trung bình cộng của tọa độ x của A và B, tức là: xF = (x1 + x2) / 2.
Tọa độ y của F bằng trung bình cộng của tọa độ y của A và B, nghĩa là: yF = (y1 + y2) / 2.
Vì vậy, tọa độ của E là E((x1 + x3) / 2, (y1 + y3) / 2), và tọa độ của F là F((x1 + x2) / 2, (y1 + y2) / 2).
Bài tập thực hành về đường trung tuyến
Xem thêm : Đá quý là gì? 8 loại đá quý trang sức phổ biến, được ưa chuộng nhất
Để nắm vững kiến thức về đường trung tuyến và vận dụng vào thực tế, chúng ta cần luyện tập thông qua các bài tập. Với kiến thức về đường trung tuyến là gì và công thức tính toán, bây giờ chúng ta sẽ vận dụng và giải hai bài tập liên quan đến đường trung tuyến.
Bài tập 1: Tính tọa độ điểm giữa cạnh BC và cạnh AC
Cho tam giác ABC có tọa độ các đỉnh A(1;2), B(3;4) và C(5;6). Tính tọa độ trung điểm giữa cạnh BC và cạnh AC.

Câu trả lời:
Để tính tọa độ trung điểm của cạnh BC, ta lấy trung bình tọa độ x và y của hai đỉnh B và C. Ta có: M((3+5)/2; (4+6)/2) = M(4;5).
Để tính tọa độ trung điểm của cạnh AC, ta lấy trung bình tọa độ x và y của hai đỉnh A và C. Ta có: N((1+5)/2; (2+6)/2) = N(3;4)
Vậy tọa độ trung điểm của cạnh BC là M(4;5) và tọa độ trung điểm của cạnh AC là N(3;4).
Bài tập 2: Tính tọa độ các đỉnh B và C dựa vào đường trung tuyến AM
Cho tam giác ABC có đỉnh A tọa độ A(2;3) và tọa độ trung điểm của cạnh BC là M(4;5). Biết rằng đường trung tuyến AM có phương trình y = 2x – 1. Tính tọa độ các đỉnh B và C.

Câu trả lời:
Để tính tọa độ của các đỉnh B và C, chúng ta cần tìm phương trình của cạnh BC. Chúng ta có thông tin sau:
- Cạnh BC vuông góc với đường trung tuyến AM nên độ dốc của cạnh BC là -1/2 (lấy số nghịch đảo của độ dốc AM).
- Cạnh BC đi qua điểm M(4;5) nên phương trình cạnh BC có dạng y = -1/2x + b.
- Thay tọa độ điểm M vào phương trình, ta được b = 7. Vậy phương trình cạnh BC là y = -1/2x + 7.
Bây giờ, ta có thể giải hệ phương trình cạnh BC và đường trung tuyến AM để tìm tọa độ các đỉnh B và C. Ta có y = -1/2x + 7 y = 2x – 1 và ta thu được x = 2 và y = 3. Do đó, tọa độ của đỉnh B hoặc đỉnh C là (2;3).
Để tìm tọa độ của đỉnh còn lại, ta sử dụng tính chất của trung điểm. Ta có: M là trung điểm của BC, do đó tọa độ x và y của M bằng trung bình cộng của tọa độ x và y của B và C. Từ đó ta suy ra 4 = (2 + x)/2 5 = (3 + y)/2
Giải hệ phương trình, ta được x = 6 và y = 7 là tọa độ của đỉnh còn lại. Vậy tọa độ của đỉnh B là (2;3) và tọa độ của đỉnh C là (6;7) hoặc ngược lại.
Kết luận
Qua bài viết này, chúng ta đã hiểu được đường trung tuyến là gì và một số thông tin chi tiết khác về đoạn thẳng này. Để nắm vững kiến thức về đường trung tuyến, chúng ta cần ôn tập và luyện tập thường xuyên các bài tập về đường thẳng này, đặc biệt là các dạng bài tập thường gặp. Hy vọng bài viết này sẽ giúp ích cho các bạn trong việc học tập và nâng cao kỹ năng giải toán hình học.
Xem thêm:
Công thức tính diện tích hình vuông chính xác nhất
Số thực là gì? Một số dạng toán học phổ biến của số thực
Nguồn: https://tuyengiaothudo.vn
Danh mục: Hỏi Đáp