Công thức tính diện tích hình vuông chính xác nhất

Công thức tính diện tích hình vuông có tính ứng dụng rất cao, cả về mặt học tập lẫn thực hành. Do đó, các em học sinh cần nắm vững công thức này để giải các bài toán yêu cầu tính diện tích hình vuông. Trong bài viết này, tuyengiaothudo.vn sẽ cung cấp công thức chính xác và hướng dẫn giải một số bài toán thường gặp, mời các bạn tham khảo tại đây!

Hình vuông là gì?

Hình vuông là một hình học quen thuộc, hình này không chỉ thường gặp trong các bài toán mà còn được ứng dụng khá nhiều trong cuộc sống. Vậy nên trước khi đến với công thức tính diện tích hình vuông, chúng ta sẽ cùng tìm hiểu về khái niệm hình học này nhé.

Bạn đang xem: Công thức tính diện tích hình vuông chính xác nhất

Hình vuông là hình tứ giác có bốn cạnh bằng nhau và bốn góc vuông bằng 90 độ.

Hình vuông là hình tứ giác có tổng cộng 4 cạnh. Sự khác biệt lớn nhất giữa hình vuông và các hình tứ giác khác là:

• Hình vuông có bốn cạnh bằng nhau.
• 4 góc được tạo thành từ 4 cạnh bằng nhau, nghĩa là hình vuông có 4 góc vuông.
• Trong hình vuông, hai cặp cạnh đối diện có độ dài bằng nhau và song song với nhau.

Khi một trong các điều kiện trên được đáp ứng, chúng ta có thể gọi tứ giác đó là hình vuông. Ví dụ, với hình vuông XYML bên dưới, chúng ta có 4 cạnh bằng nhau (XY = YM = ML = LX) và 4 góc vuông (góc X, góc Y, góc M và góc L) bằng 90 độ.

Tìm hiểu các tính chất của hình vuông

Để nhận biết một hình vuông hay không và áp dụng công thức tính diện tích hình vuông, bạn cần dựa vào các tính chất và dấu hiệu nhận biết sau:

Thiên nhiên

Các tính chất của hình vuông là:

• Hai đường chéo của hình vuông có độ dài bằng nhau và cắt nhau tại trung điểm của chúng. Đồng thời, khi hai đường chéo gặp nhau thì chúng sẽ vuông góc với nhau.
• Đường tròn nội tiếp có tâm trùng với tâm đường tròn ngoại tiếp và trùng tại giao điểm của hai đường chéo trong hình vuông.
• Mỗi đường chéo chia hình vuông thành hai hình tam giác bằng nhau.
• Hình vuông cũng có các tính chất của các hình tứ giác khác như hình bình hành, hình thoi và hình chữ nhật.

Hình vuông có hai đường chéo bằng nhau, cắt nhau tại điểm giữa và vuông góc với nhau.

Dấu hiệu để nhận biết hình vuông

Thông qua các dấu hiệu sau đây, bạn có thể nhận biết một tứ giác có phải là hình vuông hay không:

• Nếu một hình chữ nhật có hai cạnh kề nhau có độ dài bằng nhau thì có thể xác định đó là hình vuông.
• Nếu một hình chữ nhật có hai đường chéo vuông góc với nhau thì có thể xác định đó là hình vuông.
• Nếu một hình thoi có góc vuông hoặc hai đường chéo của hình thoi có độ dài bằng nhau thì ta có thể xác định rằng đó là hình vuông.

Có nhiều cách để nhận biết hình vuông.

Công thức tính diện tích hình vuông

Diện tích hình vuông là diện tích mặt phẳng mà ta nhìn thấy được. Để tính diện tích hình này ta lấy cạnh x cạnh. Các cạnh của hình vuông bằng nhau nên ta chỉ cần độ dài một cạnh là có thể tính được diện tích hình vuông.

Công thức

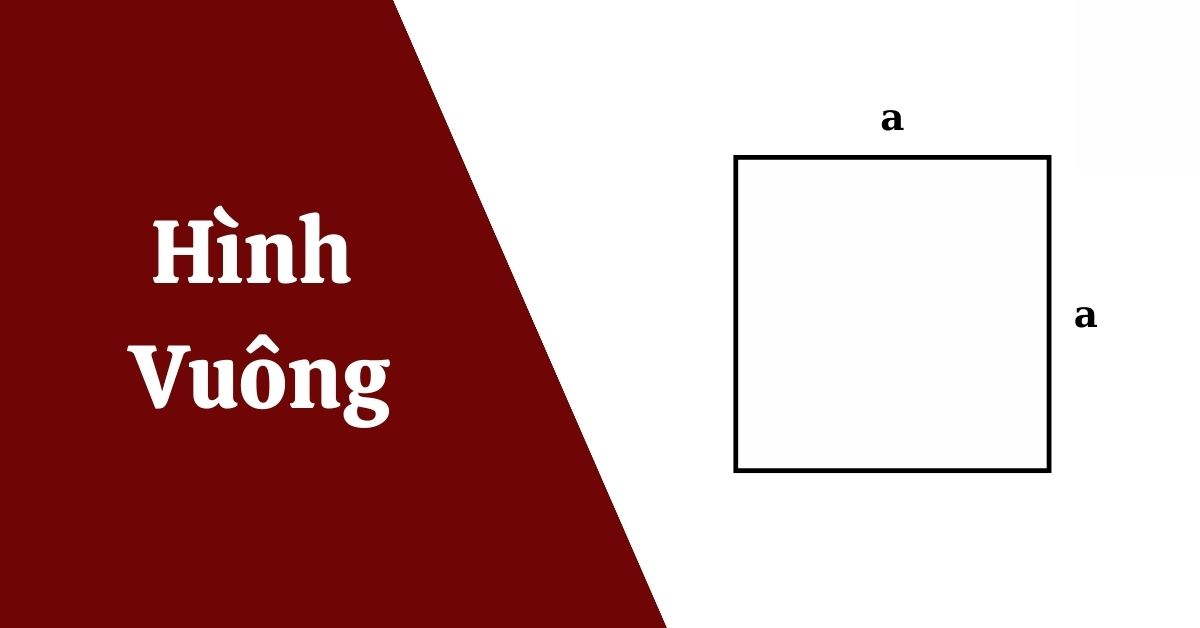
Gọi a là độ dài cạnh hình vuông, S là diện tích hình vuông, ta có công thức sau:

S = axa

Công thức tính diện tích hình vuông

Ví dụ

Ví dụ 1: Cho hình vuông XYML có độ dài cạnh bằng 5cm, hãy tính diện tích XYML.

Chúng ta có thể giải như sau:

Giải pháp

Diện tích hình vuông XYML là:

5 x 5 = 25 (cm2).

Trả lời: 25 (cm2).

Ví dụ 2: Cho hình vuông XYML có cạnh dài 10cm, hãy tính diện tích hình vuông XYML?

Giải pháp:

Diện tích hình XYML là:

10 x 10 = 100 (cm2).

Trả lời: 100 (cm2).

Một số phương pháp tính diện tích hình vuông

Như vậy, công thức cơ bản để tính diện tích hình vuông là: S = axa (cm2). Ngoài công thức chuẩn trên, bạn cũng có thể áp dụng một số cách giải khác trong trường hợp đề bài không đưa ra trực tiếp độ dài cạnh hình vuông.

Tính diện tích hình vuông bằng tổng diện tích của hai hình tam giác tạo thành từ một đường chéo

Khi ta nối hai điểm đối diện X và M trên hình vuông XYML ta sẽ tạo thành hai tam giác vuông XYM và XLM. Như vậy diện tích hình vuông sẽ bằng tổng diện tích của hai tam giác.

Công thức tính toán hiện nay là: SXYML = SXYM + SXLM = ½ x a2 + ½ x a2 (cm2).

Diện tích hình vuông bằng tổng diện tích của hai hình tam giác tạo bởi một đường chéo.

Tính diện tích hình vuông bằng tổng diện tích của hai hình chữ nhật.

Xem thêm : Tuổi Mậu Ngọ 1978 hợp số nào? Chọn số phong thủy hợp tuổi, hợp mệnh

Khi chia một hình vuông thành 2 hình chữ nhật bằng đoạn thẳng AB thì diện tích hình vuông sẽ bằng tổng diện tích của 2 hình chữ nhật:

SXYML = SXABL + SAYMB = XA x AB + AY x AB

Diện tích hình vuông bằng tổng diện tích của hai hình chữ nhật.

Tính diện tích hình vuông bằng công thức tính diện tích hình thoi

Hình vuông được coi là một dạng đặc biệt của hình thoi có 4 góc vuông và 4 cạnh bằng nhau. Do đó, bạn vẫn có thể tính diện tích hình vuông bằng công thức hình thoi nếu bạn được cung cấp độ dài đường chéo. Công thức cụ thể là:

S = ½ (XM x YL) (cm2).

Công thức tính diện tích hình thoi có thể áp dụng cho hình vuông.

Trong đó, XM và YL là 2 đường chéo của hình vuông. Trong hình vuông, 2 đường chéo có độ dài bằng nhau, do đó bạn chỉ cần độ dài của 1 đường thẳng là có thể sử dụng công thức này.

Một số điều cần biết khi tính diện tích hình vuông

Dưới đây là một số lưu ý bạn cần chú ý khi áp dụng công thức tính diện tích hình vuông ở trên.

• Khi tính toán, các cạnh phải có cùng đơn vị đo (như m2, cm2…). Đây là nguyên tắc áp dụng cho mọi công thức tính toán trong toán học, mọi hình vẽ phải có cùng đơn vị đo, nếu đề bài đưa ra các đơn vị đo khác nhau, bạn phải đổi về một đơn vị chung như cm2, m2… rồi thực hiện các bước tính toán khác nhau.
• Khi tính diện tích hình vuông (hoặc bất kỳ diện tích hình học nào), bạn sử dụng đơn vị đo diện tích như cm2 hoặc m2, chúng ta không sử dụng các đơn vị diện tích thông dụng như m, cm…
• Cần hiểu rõ và phân biệt công thức tính diện tích và chu vi. Hai công thức này thường bị nhầm lẫn, dẫn đến kết quả không chính xác ảnh hưởng đến toàn bộ bài toán.
• Bạn có thể sử dụng các công thức và tính chất của các tứ giác khác như hình chữ nhật, hình thang và hình thoi để tính diện tích hình vuông nếu đề bài không cung cấp độ dài các cạnh.

Các tham số phải có cùng đơn vị đo lường.

Bài tập tính diện tích hình vuông

Dưới đây là một số bài tập phổ biến để tính diện tích hình vuông:

Bài tập 1

Cho hình thoi XYML có góc XYM = 90 độ, độ dài cạnh XY là 8cm. Tính diện tích hình thoi XYML?

Giải pháp:

Theo dữ liệu cho sẵn, XYML là hình thoi có 1 góc vuông nên được coi là hình vuông. Do đó, bạn có thể áp dụng công thức hình vuông cho XYML có độ dài cạnh là 8cm. Ta có:

SXYML= XY x XY = 8 x 8 = 64 (cm2).

Bài tập 2

Giả sử có một tờ giấy hình vuông, mỗi cạnh dài 100mm, hãy tính diện tích tờ giấy đó theo cm2.

Giải pháp:

Để tính diện tích theo cm2, bạn cần phải đổi 100mm sang cm. Ta có: 100mm = 10cm. Khi đó, diện tích của tờ giấy sẽ là: 10 x 10 = 100 (cm2).

Bài tập 3

Cho hình vuông ABCD có chu vi là 4dm4cm, hãy tính diện tích hình vuông đó:

Giải pháp:

Đầu tiên, bạn cần phải chuyển đổi 4dm4cm sang một đơn vị nhất định, ở đây chúng ta chọn đơn vị cm: 4dm4cm = 44cm. Trong đó, chu vi hình vuông được tính bằng cạnh x 4, do đó cạnh = chu vi: 4 = 44 : 4 = 11 (cm).

Khi đó ta có cạnh hình vuông là 11 (cm), áp dụng công thức tính diện tích sẽ ra diện tích hình vuông ABCD.

Diện tích hình ABCD là 11 x 11 = 121 (cm2).

Bài tập 4

Ghép 9 mảnh giấy vuông có cạnh mỗi bên là 5cm thành một hình chữ nhật, tính diện tích hình chữ nhật đó.

Giải pháp:

Để tính diện tích hình chữ nhật, bạn cần tính tổng diện tích của mỗi hình vuông nhỏ. Diện tích của một tờ giấy là: 5 x 5 = 25 (cm2).

Hình chữ nhật được tạo thành từ 6 hình vuông nên diện tích hình chữ nhật là: 25 x 9 = 225 (cm2).

Bài tập 5

Xem thêm : Cách cài nhạc chờ Viettel

Cho chu vi hình vuông là 72cm, hãy tính diện tích hình vuông đó.

Giải pháp:

Công thức tính chu vi hình vuông là: Chu vi = cạnh x 4 => Cạnh = chu vi : 4.

Vậy cạnh hình vuông là: 72 : 4 = 18 (cm).

Vậy diện tích hình vuông sẽ là: 18 x 18 = 324 (cm2).

Bài tập 6

Cho một miếng nhựa hình vuông có mỗi cạnh dài 120mm, hãy tính S theo cm?

Giải pháp:

Đầu tiên, bạn cần phải chuyển đổi mm sang cm, chúng ta có 120mm = 12cm.

Sau khi có cạnh vuông, bạn có thể tính diện tích của miếng nhựa như sau:

12 x 12 = 144 (cm2).

Bài tập 7

Cho chu vi hình vuông ABCD là 40cm, hãy tính diện tích hình vuông ABCD:

Giải pháp:

Tương tự như các bài tập trên về chu vi hình vuông, bạn sẽ áp dụng công thức tính chu vi để tìm độ dài cạnh. Trong đó, độ dài cạnh = chu vi : 4 = 40 : 4 = 10 (cm).

Vậy diện tích hình ABCD là: 10 x 10 = 100 (cm2).

Bài tập 8

Cho một mảnh đất có 4 cạnh bằng nhau, mỗi cạnh dài 15m, hãy tính diện tích của mảnh đất đó.

Giải pháp:

Vì mảnh đất có 4 cạnh bằng nhau nên nó là hình vuông. Khi đó, bạn có thể áp dụng công thức tính diện tích hình vuông vào bài toán này.

Diện tích đất sẽ được tính như sau:

Diện tích = 15 x 15 = 225 (m2).

Bài tập 9

Một mảnh đất ban đầu có hình vuông, sau đó mở rộng thêm 6m về một cạnh và chu vi bằng 112m. Tính diện tích mảnh đất sau khi mở rộng diện tích?

Giải pháp:

Đầu tiên, bạn cần tính chu vi của ô vuông trước khi mở rộng. Chu vi này sẽ bằng chu vi tổng thể – chu vi mở rộng = 112 – 6 x 2 = 100 (m).

Khi đó, ta có chiều dài của thửa đất hình vuông ban đầu: Chu vi: 4 = 100 : 4 = 25 (m). Sau khi có chiều dài của thửa đất hình vuông, ta có chiều dài của thửa đất sau khi mở rộng: 25 + 6 = 31 (m).

Vậy diện tích mảnh đất sau khi mở rộng (bây giờ là hình chữ nhật có 1 cạnh là 25cm và 1 cạnh là 31cm) là: 25 x 31 = 775 (cm2).

Trên đây là cách tính diện tích hình vuông mà bạn có thể tham khảo. Hy vọng bài viết sẽ hữu ích và đừng quên chia sẻ cho mọi người cùng đọc nhé!

Xem thêm:

Nguồn: https://tuyengiaothudo.vn
Danh mục: Khám phá