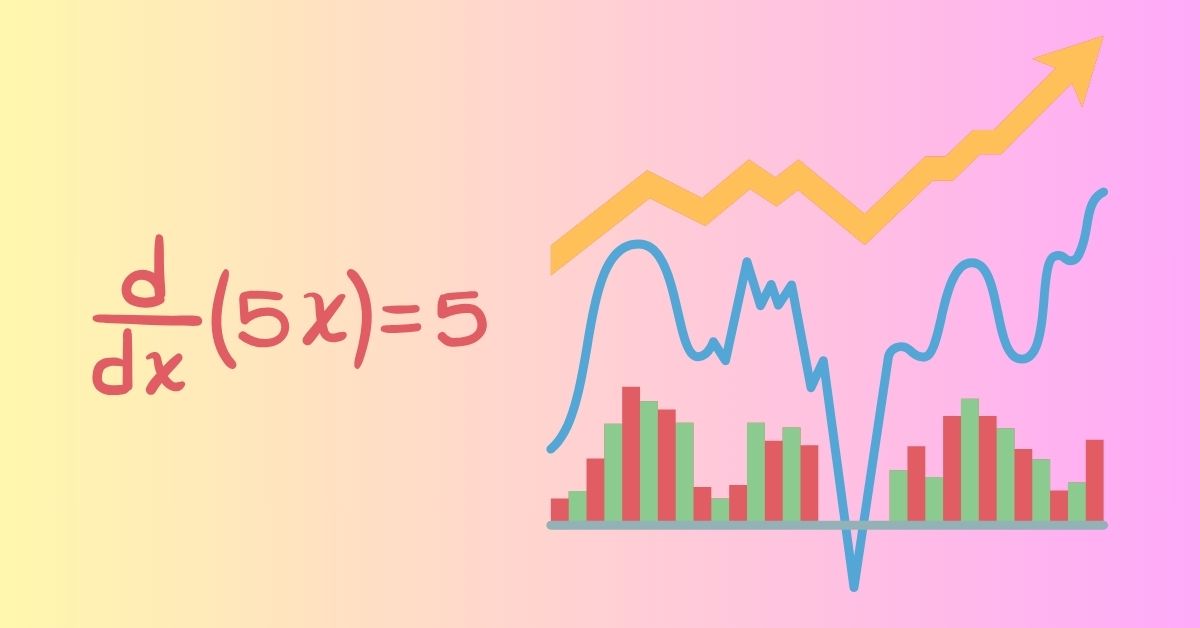Cẩm nang công thức đạo hàm và ví dụ thực tế và ứng dụng

Công thức đạo hàm đóng vai trò quan trọng và mạnh mẽ trong lĩnh vực toán học. Chúng không chỉ có giá trị lý thuyết mà còn có ảnh hưởng lớn trong nhiều lĩnh vực ứng dụng. Trong bài viết này, chúng ta sẽ khám phá sổ tay công thức đạo hàm, từ các phương pháp cơ bản đến các ứng dụng thực tế của chúng. Đồng thời, chúng ta sẽ đi sâu vào các phương pháp tính đạo hàm phổ biến, khám phá các ví dụ thực tế và các ứng dụng thú vị.

Công thức đạo hàm là gì?

Công thức đạo hàm là một công cụ toán học quan trọng để tính độ dốc của đường cong tại một điểm cụ thể. Đạo hàm của hàm f(x) tại điểm x=a được ký hiệu là f'(a) hoặc đơn giản là f'(x). Đạo hàm cũng cung cấp thông tin về độ dốc của đồ thị hàm tại mỗi điểm. Nếu đạo hàm dương tại một điểm, hàm đang tăng; nếu đạo hàm âm, hàm đang giảm; nếu đạo hàm bằng không, hàm có điểm cực trị. Đạo hàm của hàm có thể được tính bằng nhiều phương pháp khác nhau, nhưng công thức cơ bản nhất là:

Bạn đang xem: Cẩm nang công thức đạo hàm và ví dụ thực tế và ứng dụng

Công thức tính đạo hàm cơ bản của một số hàm số thông dụng như sau:

• Đạo hàm của hàm số hằng số: f(x) = c, với c là hằng số, đạo hàm của f(x) là f'(x) = 0.
• Đạo hàm của hàm mũ: f(x) = x^n, với n là số nguyên dương, đạo hàm của f(x) là f'(x) = nx^(n-1).
• Đạo hàm của hàm mũ tự nhiên: f(x) = e^x, đạo hàm của f(x) là f'(x) = e^x.
• Đạo hàm của hàm số sin và cos: f(x) = sin(x), f'(x) = cos(x); f(x) = cos(x), f'(x) = -sin(x).

Ngoài ra, còn có nhiều công thức đạo hàm khác cho các loại hàm khác nhau như hàm hợp, hàm mũ, hàm lượng giác, hàm mũ và nhiều hàm phức khác.

Ý nghĩa của công thức đạo hàm

Trong vật lý, công thức đạo hàm được sử dụng để tính toán vận tốc, gia tốc và các đại lượng khác khi một vật thể chuyển động. Đạo hàm cho chúng ta biết tốc độ thay đổi của một hàm tại mỗi điểm. Điều này hữu ích trong việc hiểu cách các hiện tượng trong thế giới thực thay đổi. Từ tốc độ chuyển động của các vật thể đến tốc độ tăng trưởng của dân số hoặc tốc độ thay đổi của giá cả.

Trong kinh tế, đạo hàm được sử dụng để tối ưu hóa hàm lợi nhuận và tìm giá trị lớn nhất hoặc nhỏ nhất của hàm. Công thức đạo hàm được sử dụng trong quá trình tối ưu hóa khi chúng ta cố gắng tìm giá trị lớn nhất hoặc nhỏ nhất của một hàm. Bằng cách sử dụng đạo hàm, chúng ta có thể xác định các điểm cực trị và điểm uốn của hàm. Điều này giúp tối ưu hóa các vấn đề thực tế như tối ưu hóa chi phí, tối ưu hóa hiệu suất, v.v.

Đạo hàm cũng giúp chúng ta hiểu rõ hơn về tính chất của hàm số, bao gồm đồ thị, điểm cực trị, điểm uốn và liệu hàm số đang tăng hay giảm.

Các dẫn xuất được sử dụng rộng rãi trong các lĩnh vực khoa học và kỹ thuật như vật lý, kỹ thuật điện, kỹ thuật hóa học, khoa học máy tính, kinh tế, v.v.

Công thức đạo hàm

Sau khi hiểu được ý nghĩa của đạo hàm, chúng ta sẽ chuyển sang công thức đạo hàm.

Công thức đạo hàm cơ bản

Công thức đạo hàm bậc cao

Công thức đạo hàm lượng giác

Hãy nhớ rằng có nhiều quy tắc khác nhau, chẳng hạn như quy tắc chuỗi, quy tắc nhân và quy tắc chia, để tính đạo hàm của các hàm phức tạp hơn.

Ví dụ về tính đạo hàm

Có nhiều phương pháp để tính đạo hàm của một hàm số. Mỗi phương pháp có ứng dụng riêng. Và chúng tôi sẽ đi sâu vào từng phương pháp để giúp bạn hiểu rõ hơn về cách tính đạo hàm.

Cách tính đạo hàm của hàm số mũ

Hàm mũ được biểu diễn dưới dạng f(x) = a^x, trong đó a là hằng số dương. Đạo hàm của hàm mũ được tính bằng công thức sau: f'(x) = a^x * ln(a).

Trong đó, ln(a) là logarit tự nhiên của a. Ví dụ, để tính đạo hàm của hàm số f(x) = 2^x, ta áp dụng công thức trên và thu được: f'(x) = 2^x * ln(2).

Cách tính đạo hàm của hàm logarit

Hàm logarit tự nhiên được biểu diễn là f(x) = ln(x). Công thức đạo hàm của hàm logarit được tính như sau: f'(x) = 1/x

Ví dụ, để tính đạo hàm của hàm số f(x) = ln(x), ta áp dụng công thức trên và có: f'(x) = 1/x

Xem thêm : Hình nền công chúa, bức tranh tuyệt vời của vẻ đẹp độc đáo

Các hàm lượng giác có thể là sin(x), cos(x) hoặc tan(x). Đạo hàm của các hàm sin(x) và cos(x) được tính bằng các công thức sau: f'(x) = cos(x) (nếu f(x) = sin(x)) f'(x) = -sin(x) (nếu f(x) = cos(x))

Đạo hàm của hàm tan(x) được tính như sau: f'(x) = sec^2(x)

Trong đó, sec(x) là hàm secant, được định nghĩa là sec(x) = 1/cos(x). Ví dụ, để tính đạo hàm của hàm f(x) = sin(x), ta áp dụng công thức trên và thu được: f'(x) = cos(x)

Cách tính đạo hàm của một hàm hợp

Một hàm hợp là một hàm được hình thành bằng cách kết hợp các hàm khác lại với nhau. Đạo hàm của một hàm hợp được tính bằng cách sử dụng quy tắc chuỗi. Quy tắc chuỗi nêu rằng đạo hàm của một hàm hợp f(g(x)) được tính bằng cách nhân đạo hàm của hàm ngoài f với đạo hàm của hàm trong g.

Ví dụ, để tính đạo hàm của hàm số f(x) = sin(2x), ta áp dụng quy tắc chuỗi và có: f'(x) = cos(2x) * 2

Trong trường hợp này, đạo hàm của hàm ngoài f là cos(x), và đạo hàm của hàm trong g là 2x (vì g(x) = 2x). Do đó, tích của hai đạo hàm này là cos(2x) * 2.

Vậy là qua các ví dụ trên, chúng ta đã thấy cách tính đạo hàm của các hàm số thông dụng và cách áp dụng chúng vào thực tế. Hiểu được đạo hàm và cách áp dụng chúng sẽ giúp chúng ta giải quyết các bài toán liên quan đến tốc độ, gia tốc, tối ưu hóa và nhiều lĩnh vực khác.

Minh họa công thức đạo hàm

Vì vậy, bạn có thể hình dung được các đạo hàm được sử dụng để làm gì và chúng được áp dụng như thế nào. Hãy đọc phần này để hiểu rõ hơn.

Tính toán tốc độ và gia tốc

Trong vật lý, đạo hàm được sử dụng để tính tốc độ và gia tốc của một vật thể. Tốc độ của một vật thể có thể được xác định bằng đạo hàm của vị trí của nó theo thời gian. Trong khi gia tốc có thể được tính bằng đạo hàm của tốc độ của nó theo thời gian.

Ví dụ, nếu vị trí của một vật được mô tả bởi hàm s

Nguồn: https://tuyengiaothudo.vn
Danh mục: Khám phá