Công thức tính chu vi và đường chéo của hình vuông không chỉ là một khái niệm cơ bản mà còn là một kỹ năng quan trọng được ứng dụng rộng rãi trong nhiều lĩnh vực. Theo đó, việc hiểu được công thức này sẽ giúp người dùng có được nền tảng kiến thức vững chắc. Đồng thời, giúp bạn có thể áp dụng nhanh chóng trong những trường hợp cần thiết. Tuy nhiên, dưới đây là cách tính chu vi hình vuông và đường chéo của chúng được tạo thành từ tuyengiaothudo.vn mà bạn có thể tham khảo.
Chu vi hình vuông là bao nhiêu?
Để hiểu cách tính chu vi hình vuông, trước tiên bạn cần hiểu định nghĩa và bản chất của hình học này. Cụ thể, dưới đây chúng tôi sẽ cung cấp một số thông tin cần thiết để bạn có thể dễ dàng tiếp cận phép tính này hơn.
Bạn đang xem: Cách tính chu vi, đường chéo hình vuông chính xác nhất
Định nghĩa cơ bản về chu vi hình vuông
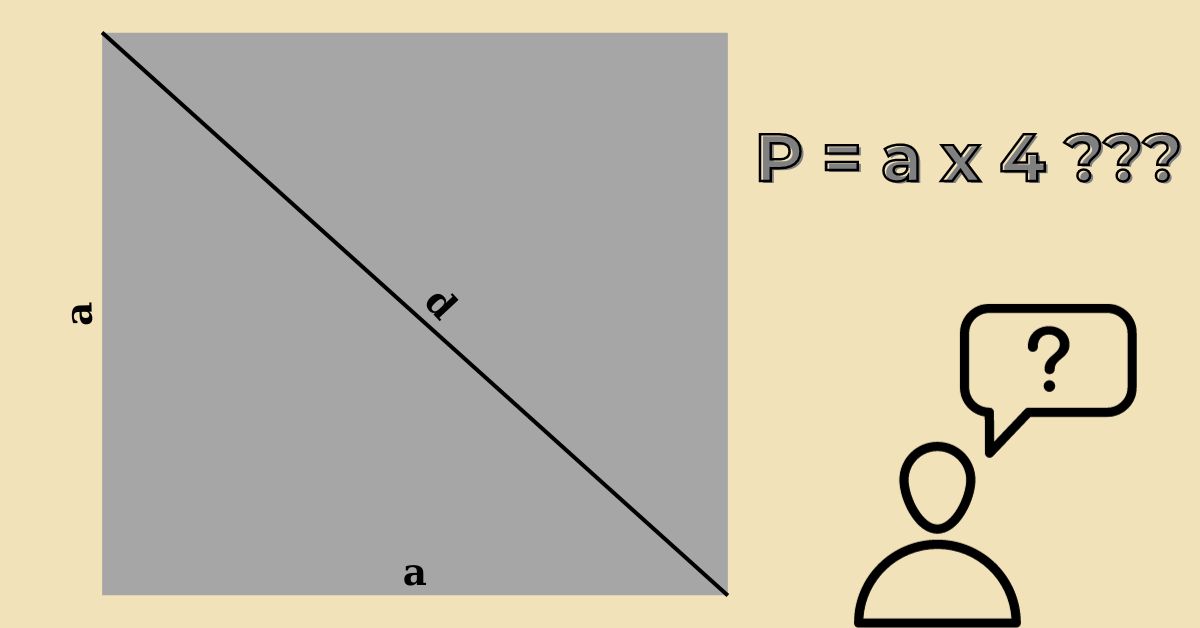
Về cơ bản, chu vi của hình vuông là tổng độ dài của tất cả các cạnh của hình. Tuy nhiên, đối với hình vuông, mỗi cạnh thường bằng nhau, vì vậy cách tính chu vi của hình vuông là nhân độ dài của một cạnh với 4. Đặc biệt, đơn vị đo chu vi thường được biểu thị bằng đơn vị độ dài cạnh, chẳng hạn như cm hoặc mét.

Trên thực tế, chu vi là một tính chất quan trọng của hình vuông và thường được sử dụng trong nhiều lĩnh vực từ hình học đến xây dựng và thiết kế. Chúng không chỉ giúp người dùng tiết kiệm thời gian xác định độ dài của vật thể cần tính toán mà còn đóng vai trò quan trọng trong việc đẩy nhanh tiến độ công việc. Tuy nhiên, để sử dụng hiệu quả các tính chất của chu vi hình vuông, bạn nên tìm hiểu thêm về các công thức của chúng trong nội dung sau.
Công thức cơ bản và cách tính chu vi hình vuông dành cho bạn
Công thức và phương pháp tính chu vi hình vuông thực tế được áp dụng trong nhiều lĩnh vực khác nhau. Trong đó, toán học có lẽ là lĩnh vực thường được áp dụng công thức này. Bởi vì, đó là những kỹ năng và kiến thức cơ bản mà mọi học sinh phải nắm vững để giải quyết những câu hỏi khó hơn.

Dưới đây là công thức tính chu vi hình vuông chi tiết mà bạn có thể tham khảo:
Chu vi = Độ dài cạnh x Số cạnh
Theo đó:
- Chu vi là tên gọi riêng của tổng chiều dài các cạnh của hình vuông.
- Độ dài cạnh là kích thước của mỗi cạnh hình vuông, thường được ký hiệu là a.
- Số cạnh là số cạnh của một hình vuông và một hình vuông sẽ có 4 cạnh.
Hình minh họa: Giả sử chúng ta có một hình vuông có cạnh a = 5 cm. Để tính chu vi của hình vuông này, chúng ta áp dụng công thức cho ở trên:
Xem thêm : Đấu La Đại Lục: Hồn Sư Đối Quyết
Chu vi = Độ dài cạnh x Số cạnh = 5 x 4 = 20 cm.
Ghi chú: Vì mỗi cạnh đều bằng nhau và hình vuông có 4 cạnh nên chu vi của hình vuông này là 20 cm. Đây là ví dụ về cách tính chu vi hình vuông dựa trên công thức cơ bản. Theo đó, bạn cũng có thể sử dụng công thức và cách tính chu vi hình vuông trong ví dụ này để tính tất cả các hình học hình vuông khác trong các bài toán khác.
Lưu ý khi tính chu vi hình vuông
Quá trình thực hiện công thức tính chu vi hình vuông có vẻ đơn giản, nhưng thực tế rất khó để thực hiện và đưa ra kết quả đúng nếu bạn xác định hoặc tính toán dữ liệu sai. Để hạn chế các trường hợp trên, bạn có thể đọc qua một số điều cần lưu ý dưới đây.

- Trong các câu hỏi thi có nhiều hình vuông, bạn cần xác định độ dài chính xác của cạnh hình vuông mà bạn cần tính toán. Đồng thời, bạn cần đảm bảo rằng bạn đã đo chính xác độ dài cạnh bằng các công cụ đo thích hợp như thước kẻ hoặc thước kẻ.
- Trong quá trình tính toán, bạn cũng nên tránh làm tròn số quá nhiều, đặc biệt là khi đo bằng các đơn vị nhỏ như milimét. Bởi vì, rất có thể dữ liệu này sẽ ảnh hưởng đến kết quả tính toán của các câu hỏi khác trong bài kiểm tra.
- Nếu có thể, bạn nên sử dụng các công cụ hỗ trợ như máy tính hoặc ứng dụng tính toán để giảm thiểu lỗi trong quá trình tính toán. Thậm chí so sánh câu trả lời của bạn với dữ liệu thực tế đã đo được để kiểm tra độ chính xác của dự án.
- Ngoài ra, hãy đảm bảo bạn chỉ định đơn vị đo lường mà bạn đang sử dụng và đảm bảo rằng cả độ dài cạnh và kết quả chu vi đều được thể hiện theo cùng một đơn vị. Đây là một trong những lỗi thường gặp của học sinh khi giải câu đố. Vì vậy, hãy kiểm tra cẩn thận trước khi đưa ra kết quả cuối cùng của bạn.
Ứng dụng tính chu vi hình vuông trong thực tế
Cách tính chu vi hình vuông có nhiều ứng dụng thực tế trong nhiều lĩnh vực khác nhau. Sau đây là một số ví dụ về cách áp dụng kiến thức về chu vi hình vuông mà bạn không thể bỏ qua.

- Chu vi hình vuông là một phần cơ bản của hình học và toán học. Nó giúp học sinh hiểu mối quan hệ giữa các khái niệm cơ bản như chu vi, diện tích và độ dài cạnh.
- Trong ngành xây dựng, chu vi hình vuông được sử dụng để tính lượng vật liệu cần thiết để xây tường vuông góc, sàn nhà hoặc các cấu trúc khác.
- Chu vi của hình vuông cũng được sử dụng để tính diện tích khi kết hợp với chiều rộng hoặc chiều dài. Điều này có thể hữu ích trong quản lý và đo lường đất đai, đặc biệt là khi xác định diện tích đất trong một dự án bất động sản.
- Trong lĩnh vực thiết kế đồ họa, kiến thức về cách tính chu vi hình vuông được coi là quan trọng trong việc xác định kích thước và tỷ lệ của các đối tượng. Đây là nền tảng để tạo ra các bản vẽ kỹ thuật và đồ họa chất lượng cao ngày nay.
Đường chéo của hình vuông là bao nhiêu?
Tương tự như tính chu vi hình vuông, để thực hiện phép tính đường chéo của hình học này, bạn cần nắm được các định nghĩa và lý thuyết cơ bản của chúng thông qua các gợi ý sau.
Định nghĩa cơ bản của đường chéo hình vuông
Đường chéo (d) của hình vuông được hiểu đơn giản là đường thẳng nối hai đỉnh đối diện của hình vuông. Trong hình học không gian, đường chéo chia hình vuông thành hai tam giác vuông đều. Điều này tạo ra một góc 45 độ với mỗi cạnh của hình vuông. Do đó, có thể nói rằng đường chéo là một trong những đặc điểm độc đáo của hình vuông mà các hình học khác không có.

Trong các bài toán, độ dài đường chéo cũng là một con số quan trọng trong công thức và cách tính chu vi hình vuông. Bởi vì bạn sẽ phải dựa vào độ dài đường chéo để tính độ dài cạnh của hình học. Do đó, trong các bài toán hay trong các lĩnh vực như trắc địa, xây dựng và thiết kế, việc tính toán nét cũng được coi là một yếu tố cơ bản giúp người thực hiện tối đa hóa thời gian thực hiện.
Công thức và cách tính đường chéo của hình vuông dành cho bạn
Để tính độ dài đường chéo (d) trong hình vuông, bạn có thể sử dụng công thức Pythagoras. Bởi vì đây là đường chéo tạo ra hai tam giác vuông đều. Cụ thể, công thức tính này sẽ được trình bày chi tiết như sau:
d² = Một² + b²
Xem thêm : Hình ảnh đẹp của cặp đôi yêu nhau
Trong đó:
- d là độ dài đường chéo.
- a và b là độ dài của các cạnh kề của hình vuông. Thông thường, độ dài của hai cạnh này sẽ bằng nhau.
Hình minh họa: Giả sử chúng ta có một hình vuông có cạnh dài 6 cm. Tính đường chéo và chu vi của hình vuông trên.
Câu trả lời:
Áp dụng công thức Pythagoras, ta có thể tính độ dài đường chéo như sau:
d² = a² + b² = 6² + 6² = √72 = 8,49 cm
Theo đó, việc tính chu vi hình vuông sẽ được thực hiện theo công thức sau:
Chu vi = Độ dài cạnh x Số cạnh = 6 x 4 = 24 cm.
Ghi chú: Tính đường chéo và chu vi hình vuông sẽ có những lưu ý tương tự. Do đó, bạn cũng có thể tham khảo nội dung tương tự trong phần lưu ý khi tính chu vi hình vuông để quá trình tính toán chính xác và nhanh hơn.
Ứng dụng của đường chéo hình vuông trong thực tế
Tính toán đường chéo của hình vuông có nhiều ứng dụng thực tế, đặc biệt là trong các lĩnh vực liên quan đến khảo sát, xây dựng và thiết kế. Dưới đây là một số ví dụ về cách áp dụng kiến thức về đường chéo của hình vuông vào thực tế mà bạn có thể tham khảo.

- Trong ngành xây dựng, phương pháp đường chéo vuông góc được sử dụng để xác định độ dài đường chéo của các diện tích vuông góc. Ví dụ, khi xây dựng một bức tường chéo giữa hai bức tường vuông góc. Chúng cũng được sử dụng rộng rãi trong việc tính toán chu vi của một hình vuông. Điều này có thể hữu ích trong việc đo đất, kích thước của các phòng hoặc diện tích của bất kỳ hình vuông nào.
- Trong lĩnh vực thiết kế nội thất, đường chéo của hình vuông thường được sử dụng để tạo ra các đường chéo trong bố cục của các vật dụng nội thất, giúp tăng cường sự cân bằng và tính thẩm mỹ trong quá trình gia công.
- Ngoài ra, trong các bài toán hình học và hình học không gian, công thức tính đường chéo hình vuông cũng được sử dụng rất linh hoạt, chúng hầu như giải quyết được mọi bài toán về kích thước và vị trí hình vuông, giúp bạn giải nhanh các bài toán khó.
Lời kết
Đó là cách tính chu vi hình vuông và đường chéo của chúng chính xác nhất mà bạn có thể tham khảo và áp dụng ngay vào bài tập của mình. Qua bài viết hôm nay, tuyengiaothudo.vn Hy vọng bạn sẽ nắm được những phép tính cơ bản được giới thiệu ở trên. Đồng thời, bạn có thể nâng cao vị thế và thành tích của mình trong quá trình học tập.
XEM THÊM
Nguồn: https://tuyengiaothudo.vn
Danh mục: Khám phá