Khi làm quen với một loại hình học bất kỳ, các bạn học sinh đều phải học qua về cách tính chu vi của loại hình đó. Công thức tính chu vi là nội dung thiết yếu mà bạn cần phải nắm vững để có thể giải nhiều bài toán từ đơn giản đến phức tạp. Hãy cùng Happymath khám phá một số công thức toán tính chu vi hình học phổ biến trong bài viết hôm nay nhé.
- Bạc 925 là gì? Giá bạc 925 có đắt không? Những điều nên biết
- Biển Số Xe 90 Thuộc Tỉnh Nào? Giải Đáp Chi Tiết
- C++ là gì? Tổng hợp kiến thức học C++ cơ bản cực dễ hiểu
- BitLocker là gì? Cách bật, tắt BitLocker có thể bạn chưa biết
- Cổng Thunderbolt là gì? So sánh tốc độ hoạt động giữa Thunderbolt 3 và 1, 2
Chu vi trong toán học
Chu vi là gì
“Chu vi” trong toán học là tổng độ dài của tất cả các cạnh của một hình học. Đối với các hình học đơn giản như hình vuông, hình chữ nhật, tam giác, hay các hình dạng phức tạp hơn như đa giác, chu vi là một khái niệm quan trọng để đo lường và mô tả kích thước của hình đó.
Bạn đang xem: TỔNG HỢP CÔNG THỨC TOÁN TÍNH CHU VI HÌNH HỌC
Chúng ta thường sử dụng kí hiệu P (Perimeter) hoặc C (Circumference) để biểu diễn chu vi và đơn vị đo lường chiều dài (thường là mét hoặc centimet).
Vai trò của tính chu vi trong toán hình học
Có thể thấy, chu vi là một trong những khái niệm cơ bản nhất mà bạn cần nắm vững khi học toán. Bởi lẽ vai trò của chu vi không chỉ là một phép tính mà còn hữu dụng xuyên suốt quá trình học tập:
- Đo lường kích thước: Chu vi là một phương tiện đo lường để xác định kích thước của các hình học. Nó giúp chúng ta hiểu rõ về độ dài của các cạnh, đoạn thẳng và đường tròn.
- Quyết định định hình: Chu vi là một đặc điểm quan trọng để nhận biết và phân loại các hình học. Nó giúp xác định sự đối xứng, tỉ lệ, và các đặc tính hình dạng của các đối tượng.
- Giải quyết vấn đề hình học: Trong nhiều bài toán hình học, tính chu vi đóng vai trò quan trọng trong quá trình giải quyết vấn đề. Cụ thể, khi cần tối ưu hóa hay tìm giá trị cực tiểu, tính chu vi thường được sử dụng như một hàm mục tiêu.
- Ứng dụng trong lĩnh vực số học và tính toán: Tính chu vi thường xuất hiện trong nhiều công thức và phương trình toán học, đặc biệt là khi tính diện tích, thể tích, hay trong các bài toán tính toán phức tạp hơn.
Chu vi trong toán học
Xem thêm: Tìm hiểu các loại góc hình học trong toán tiếng anh
Những hình học quan trọng
Có rất nhiều loại hình học khác nhau mà bạn sẽ được tiếp cận trong môn toán. Hãy cùng Happymath xem qua các hình học quan trọng cần ghi nhớ nhé:
- Hình vuông (Square): Một hình vuông có cạnh bằng và góc vuông 90 độ. Có các tính chất đặc biệt như đường chéo bằng nhau và là một dạng đặc biệt của hình chữ nhật.
- Hình chữ nhật (Rectangle): Một hình chữ nhật có góc vuông và các cạnh đối diện bằng nhau.
- Tam giác (Triangle): Một tam giác có ba cạnh và ba góc. Có nhiều loại tam giác như tam giác vuông, tam giác cân, và tam giác đều.
- Hình thang (Trapezoid): Một hình thang có hai cạnh song song và hai cạnh không song song.
- Hình tròn (Circle): Một hình tròn có tất cả các điểm trên bề mặt cách đều từ một điểm gọi là trung tâm.
- Đa giác (Polygon): Đa giác là một hình đa diện với các đỉnh và cạnh. Có nhiều loại đa giác như hình ngũ giác, hình sáu giác, và nhiều hình dạng khác.
- Hình elip (Ellipse): Một hình elip có dạng giống như hình tròn nhưng có hai bán kính khác nhau.
Các công thức tính chu vi quan trọng
Công thức tính chu vi hình tròn
Công thức: C = 2πr hay C = πd
Trong đó:
- r: bán kính của hình tròn.
- d: đường kính của hình tròn.
- π (pi) 3.14.
Công thức tính chu vi hình tròn
Ví dụ: Cho hình tròn có r = 5. Tính chu vi của hình tròn.
Hướng dẫn:
C = 2πr
C=2π×5
C≈31.41
Công thức tính chu vi hình elip
Công thức: C2(a2+b2)/2
Trong đó:
- a: bán trục chính.
- b: bán trục phụ.
Công thức tính chu vi hình elip
Ví dụ: Cho một hình elip có bán trục chính a = 5 và bán trục phụ b = 3, tính chu vi của hình elip này.
Hướng dẫn:
C2(a2+b2)/2
C 2(52+32)/2
C 234/2
C 217
C25.92
Công thức tính chu vi hình tam giác
Công thức: C = a + b + c
Xem thêm : Xuất hiện loại topping trà sữa mới toanh, dự báo còn hot hơn cả trân châu đường đen
Trong đó: a, b, c là độ dài cạnh trong tam giác.
Công thức tính chu vi hình tam giác
Ví dụ: Cho hình tam giác có a = 3, b = 4, c = 5. Tính chu của tam giác.
Hướng dẫn:
C = a + b + c
C = 3+ 4 + 5 = 12
Công thức tính chu vi hình vuông
Công thức: C = 4a
Trong đó: a là độ dài của cạnh hình vuông đó.
Công thức tính chu vi hình vuông
Ví dụ: Tính chu vi hình vuông có a = 5.
Hướng dẫn:’
C = 4a
C = 4 x 5 = 20
Công thức tính chu vi hình thoi
Công thức: C = 4a
Trong đó: a là độ dài cạnh trong hình thoi.
Công thức tính chu vi hình thoi
Ví dụ: Cho hình thoi có a = 6. Tính chu vi hình thoi này.
Hướng dẫn:
C = 4a = 4×6 = 24
Công thức tính chu vi hình bình hành
Công thức: C = (a + b) x 2
Trong đó:
- a là chiều dài của cạnh thứ nhất.
- a là chiều cạnh thứ hai, song song với a.
Công thức tính chu vi hình bình hành
Ví dụ: Tính chu vi hình bình hành có a = 4 và b = 6.
Hướng dẫn:
C = 2 x (a + b) = 2 x (4 + 6) = 2 × 10= 20
Công thức tính chu vi hình thang
Xem thêm : Viber là gì? Có tính năng gì? Sử dụng như thế nào? Có gì thú vị?
Công thức: C = a + b + c + d
Trong đó: a, b, c, d là cạnh của hình thang.
Công thức tính chu vi hình thang
Ví dụ: Tính chu vi hình thang với các độ dài tương ứng:
- a = 5
- b = 8
- c = 5
- d = 8
Hướng dẫn:
C = a + b + c + d = 5 + 8 + 5 + 8 = 26
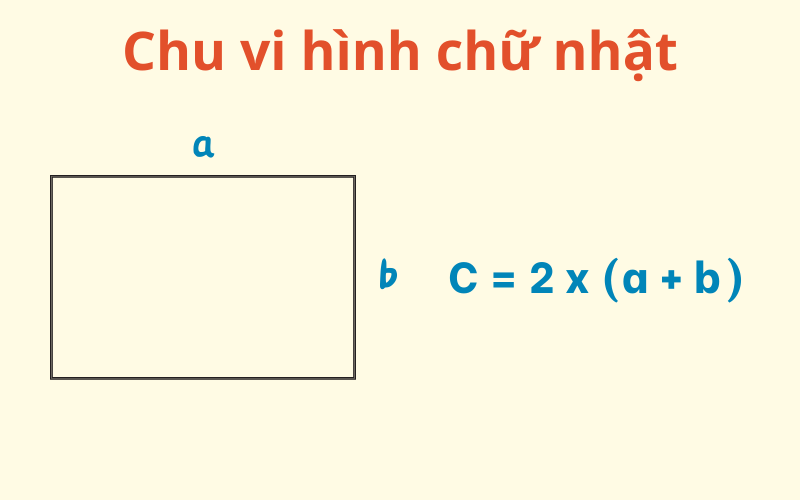
Công thức tính chu vi hình chữ nhật
Công thức: C = 2 x (a + b)
Trong đó:
- a: chiều dài.
- b: chiều rộng.
Công thức tính chu vi hình chữ nhật
Ví dụ: Tính chu vi hình chữ nhật có a = 5 và b = 3.
Hướng dẫn:
C = 2 x (a + b) = 2 x (5+3) = 16
Công thức tính chu vi hình trụ
Công thức: C = 2πr + h
Trong đó:
- r là bán kính đáy.
- h là chiều cao của hình trụ.
- π (pi) 3.14.
Công thức tính chu vi hình trụ
Ví dụ: Cho hình trụ có r = 5, h = 8. Tính chu vi hình trụ này.
Hướng dãn:
C = 2πr + h = 2π5 + 8 38.85
Công thức tính chu vi hình lục giác
Công thức: P = 6s
Trong đó: s là độ dài mỗi cạnh.
Công thức tính chu vi hình lục giác
Ví dụ: Cho hình lục giác có s = 5. Tính chu vi hình lục giác.
Hướng dẫn:
P = 6s = 6 × 5 = 30
Tổng kết
Trong bài viết này, chúng ta đã khám phá những công thức quan trọng để tính chu vi của các hình học cơ bản, như hình vuông, hình chữ nhật và thậm chí là hình lục giác. Những công thức này không chỉ giúp chúng ta đo lường và mô tả kích thước của các hình, mà còn là công cụ quan trọng trong nhiều bài toán hình học và tính toán phức tạp.
Nguồn: https://tuyengiaothudo.vn
Danh mục: Hỏi Đáp