Ở mức độ cơ bản, tỉ số lượng giác được sử dụng để giải các vấn đề hình học, như tính toán chiều dài các cạnh và đo góc trong tam giác vuông. Ngoài ra, chúng còn xuất hiện trong nhiều ứng dụng thực tế từ kỹ thuật và vật lý đến máy tính và nghệ thuật đồ họa. Trong lĩnh vực vật lý, tỉ số lượng giác giúp mô tả các quy luật đối với các vấn đề như dao động và sóng. Trong công nghệ, chúng được tích hợp trong các hệ thống điều khiển tự động, đặc biệt là trong việc điều khiển vị trí của các thiết bị như robot. Trong bài viết hôm nay chúng ta sẽ cùng tìm hiểu bảng công thức lượng giác đầy đủ cũng như những ứng dụng sâu rộng của nó trong cuộc sống.
Khái niệm tỉ số lượng giác
Tỉ số lượng giác của một góc nhọn là một khái niệm trong lượng giác được sử dụng để mô tả mối quan hệ giữa các cạnh của tam giác vuông và góc tương ứng. Tỉ số lượng giác được định nghĩa bằng phép chia của các cạnh trong tam giác vuông. Trong tam giác vuông, có bốn tỉ số lượng giác chính được xác định:
Bạn đang xem: Công thức lượng giác, bảng công thức lượng giác đầy đủ nhất
1. Tỉ số sin: Tỉ số sin của một góc (x) trong tam giác vuông bằng độ dài cạnh đối của góc chia cho độ dài cạnh huyền.
Công thức: sin(x) = cạnh đối/huyền
2. Tỉ số cos: Tỉ số cos của một góc (x) trong tam giác vuông bằng độ dài cạnh kề góc chia cho độ dài cạnh huyền.
Công thức: cos(x) = cạnh kề/huyền
3. Tỉ số tan: Tỉ số tan của một góc (x) trong tam giác vuông bằng độ dài cạnh đối của góc chia cho độ dài cạnh kề góc.
Công thức: tan(x) = cạnh đối/cạnh kề
4. Tỉ số cot: Tỉ số cot của một góc (x) trong tam giác vuông bằng độ dài liền kề chia cho độ dài cạnh đối của góc.
Công thức: cot(x) = cạnh kề/cạnh đối

Các tỉ số lượng giác này được ứng dụng để tính toán các giá trị góc, cạnh hoặc các quan hệ giữa chúng trong tam giác vuông. Chúng cũng được áp dụng rộng rãi trong các lĩnh vực như toán học, vật lý, địa hình và kỹ thuật. Về ứng dụng của các tỉ số này chúng ta sẽ tìm hiểu kỹ hơn trong nội dung cuối. Trong phần tiếp theo chúng ta sẽ lần lượt điểm qua một loạt các công thức lượng giác thường gặp nhé.
Công thức lượng giác cơ bản
sin^2(x) + cos^2(x) = 1
1/(sin^2(x)) = 1+ cot^2(x)
1/(cos^2(x)) = 1+ tan^2(x)
tan(x).cot(x) = 1
cot(x) = cos(x)/sin(x)
tan(x) = sin(x)/cos(x)

Công thức cộng lượng giác
sin(a+b) = sin(a).cos(b) + cos(a).sin(b)
sin(a-b) = sin(a).cos(b) – cos(a).sin(b)
cos(a+b) = cos(a).cos(b) – sin(a).sin(b)
cos(a-b) = cos(a).cos(b) + sin(a).sin(b)
tan(a+b) = (tan(a)+tan(b)) / (1 – tan(a).tan(b))
tan(a-b) = (tan(a)-tan(b)) / (1 + tan(a).tan(b))

Công thức lượng giác biến đổi tổng thành tích
cos(a) + cos(b) = 2cos((a+b)/2).cos((a-b)/2)
cos(a) – cos(b) = -2sin((a+b)/2).sin((a-b)/2)
sin(a) + sin(b) = 2sin((a+b)/2).cos((a-b)/2)
sin(a) – sin(b) = 2cos((a+b)/2).sin((a-b)/2)

Công thức lượng giác biến đổi tích thành tổng
cos(a).cos(b) = 1/2[cos(a+b) + cos(a-b)]
sin(a).sin(b) = -1/2[cos(a+b) – cos(a-b)]
sin(a).cos(b) = 1/2[sin(a+b) + sin(a-b)]

Các công thức nhân góc
Các công thức nhân lượng giác này được sử dụng để đơn giản hóa và tính toán các giá trị lượng giác nhân 2, nhân 3 của một góc dựa trên giá trị lượng giác của góc ban đầu.
Công thức nhân đôi
Có ba công thức đôi lượng giác nhân đôi tương ứng với các tỉ số lượng giác sin, cos và tan:
Xem thêm : 101+ hình nền hoa Tulip Full HD, 4k sắc nét đẹp nhất
Công thức sin nhân đôi: sin(2x) = 2sin(x)cos(x)
Công thức cos nhân đôi: cos(2x) = cos^2(x) – sin^2(x) = 2cos^2(x) – 1 = 1 – 2sin^2(x)
Công thức tan nhân đôi: tan(2x) = (2tan(x))/(1 – tan^2(x))

Công thức nhân ba
Có hai công thức lượng giác nhân ba chính, tương ứng với các tỉ số lượng giác sin và cos:
Công thức sin nhân ba: sin(3x) = 3sin(x) – 4sin^3(x)
Công thức cos nhân ba: cos(3x) = 4cos^3(x) – 3cos(x)
Công thức tan nhân ba: tan(3x) = (3tan(x) – tan^3(x))/(1 – 3tan^2(x))
Phép tính lượng giác các cung đặc biệt
Công thức lượng giác của các cung đặc biệt là các phép tính lượng giác áp dụng cho các góc đặc biệt như góc 0 độ, 90 độ và 180 độ. Các phép tính lượng giác của các cung đặc biệt giúp tính toán nhanh chóng các giá trị lượng giác của các góc cụ thể mà không cần dùng đến bảng giá trị hoặc máy tính. Điều này tiết kiệm thời gian và giúp tăng tốc độ giải các bài toán lượng giác. Có ba phép tính lượng giác của các cung liên quan đặc biệt, được sử dụng để tính toán các giá trị lượng giác của các cung góc đặc biệt.
Phép tính lượng giác của cung nửa đường tròn:
- sin(π/2) = 1
- cos(π/2) = 0
- tan(π/4) = 1
Khi xét một cung đầy độ trong hình tròn đơn vị, ta có:
- sin(π) = 0
- cos(π) = -1
- tan(π/2) = không tồn tại
Phép tính lượng giác của cung 0:
- sin(0) = 0
- cos(0) = 1
- tan(0) = 0

Công thức lượng giác các cung liên quan
Ngoài các phép tính lượng giác cơ bản, phép tính lượng giác các cung liên quan cũng là một phần quan trọng của toán học và được sử dụng rộng rãi trong nhiều lĩnh vực khác nhau. Dưới đây là một số phép tính lượng giác các cung liên quan khá quan trọng.
Công thức lượng giác hai cung đối nhau
Phép tính lượng giác hai cung đối nhau là một công thức quan trọng trong lượng giác, hữu ích trong việc giải các bài toán lượng giác và xác định giá trị của các cung trong các tương quan hình học và vật lý. Cụ thể, công thức này áp dụng cho các cung bù nhau tức là tổng hai góc 0 độ. Có hai phép tính lượng giác hai cung đối nhau chính cho sin và cos, sau đó phát triển thêm công thức cho tan và cot.
Phép tính lượng giác hai cung đối nhau cho sin: sin(-x) = -sin(x)
Ví dụ: sin(-π/6) = -sin(π/6)
Phép tính lượng giác hai cung đối nhau cho cos: cos(-x) = cos(x)
Ví dụ: cos(-π/4) = cos(π/4)
Phép tính lượng giác hai cung đối nhau cho tan: tan(-x) = -tan(x)
Ví dụ: tan(-π/4) = -tan(π/4)
Phép tính lượng giác hai cung đối nhau cho cot: cot(-x) = -cot(x)
Ví dụ: cot(-π/4) = -cot(π/4)
Phép tính lượng giác hai cung bù nhau
Công thức tính lượng giác hai cung bù nhau áp dụng cho các cung có tổng hai gốc bằng π hoặc bằng 180 độ. Có hai phép tính lượng giác hai cung đối nhau chính cho sin và cos, sau đó phát triển thêm công thức cho tan và cot.
Phép tính lượng giác hai cung bù nhau cho sin: sin(π – x) = sin(x)
Ví dụ: sin(π – π/6) = sin(π/6)
Phép tính lượng giác hai cung bù nhau cho cos: cos(π – x) = -cos(x)
Ví dụ: cos(π – π/4) = -cos(π/4)
Phép tính lượng giác hai cung bù nhau cho tan: tan(π – x) = -cos(x)
Ví dụ: tan(π – π/4) = -tan(π/4)
Phép tính lượng giác hai cung bù nhau cho cot: cot(π – x) = -cot(x)
Ví dụ: cot(π – π/4) = -cot(π/4)

Công thức lượng giác hai cung phụ nhau
Phép tính lượng giác hai cung phụ nhau áp dụng cho hai góc có tổng bằng 90 độ (hoặc π/2 radian). Có bốn phép tính lượng giác hai cung phụ nhau như sau.
Phép tính lượng giác hai cung phụ nhau cho sin: sin(π/2 – x) = cos(x)
Ví dụ: sin(π/2 – π/4) = cos(π/4)
Phép tính lượng giác hai cung phụ nhau cho cos: cos(π/2 – x) = sin(x)
Xem thêm : Cách đăng ký gói cước gọi nội mạng Mobi
Ví dụ: cos(π/2 – π/4) = sin(π/4)
Phép tính lượng giác hai cung phụ nhau cho tan: tan(π/2 – x) = cot(x)
Ví dụ: tan(π/2 – π/4) = cot(π/4)
Phép tính lượng giác hai cung phụ nhau cho cot: cot(π/2 – x) = tan(x)
Ví dụ: cot(π/2 – π/4) = tan(π/4)
Công thức lượng giác hai cung hơn kém π
Phép tính lượng giác hai cung hơn kém π (hay 180 độ) áp dụng cho các góc có hiệu của chúng bằng π. Có hai phép tính lượng giác hai cung hơn kém π chính:
Phép tính lượng giác hai cung hơn kém π cho sin: sin(π + x) = -sin(x)
Ví dụ: sin(π + π/6) = -sin(π/6)
Phép tính lượng giác hai cung hơn kém π cho cos: cos(π + x) = -cos(x)
Ví dụ: cos(π + π/6) = -cos(π/6)

Phép tính lượng giác hai cung hơn kém π cho sin: tan(π + x) = tan(x)
Ví dụ: sin(π + π/6) = tan(π/6)
Phép tính lượng giác hai cung hơn kém π cho cos: cot(π + x) = cot(x)
Ví dụ: cos(π + π/6) = cot(π/6)
Công thức lượng giác cung hơn kém π/2
Phép tính lượng giác hai cung hơn kém π/2 (hay 90 độ) áp dụng cho các góc có hiệu của chúng bằng π/2. Có hai phép tính lượng giác hai cung hơn kém π/2 chính:
Phép tính lượng giác hai cung hơn kém π/2 cho sin: sin(π/2 + x) = cos(x)
Ví dụ: sin(π/2 + π/4) = cos(π/4)
Phép tính lượng giác hai cung hơn kém π/2 cho cos: cos(π/2 + x) = -sin(x)
Ví dụ: cos(π/2 + π/3) = -sin(π/3)
Ứng dụng của tỉ số lượng giác
Tỉ số lượng giác được sử dụng trong lập trình để thực hiện các tính toán hình học và đồ họa. Trong nghệ thuật đồ họa số, chúng giúp tạo ra các hiệu ứng hình học và định hình không gian. Điều này làm cho tỉ số lượng giác trở thành một công cụ quan trọng, không chỉ trong lĩnh vực toán học mà còn trong nhiều khía cạnh khác của cuộc sống và khoa học ứng dụng.
Toán học
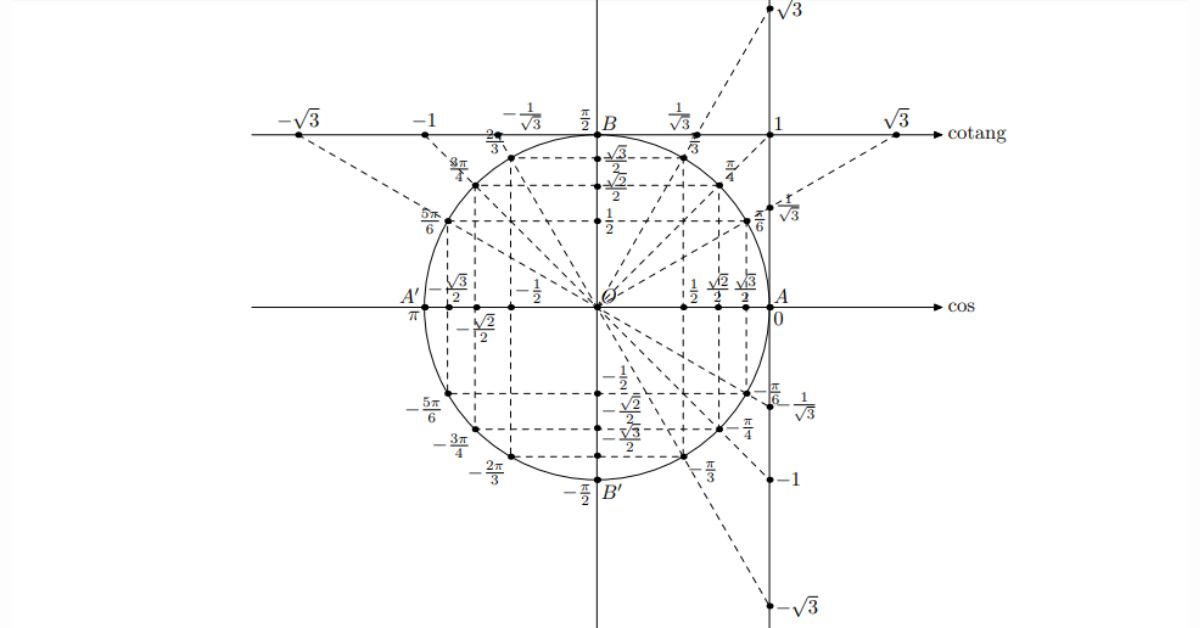
Trong toán học, một công cụ quan trọng giúp chúng ta thực hiện các phép tính liên quan đến các giá trị của các hàm lượng giác (sin, cos, tan, cot) nhanh hơn, chính xác hơn đó chính là bảng công thức lượng giác đầy đủ. Bảng công thức này chứa các giá trị lượng giác của các góc phổ biến, ví dụ như 0°, 30°, 45°, 60° và 90°, cũng như các góc có giá trị lượng giác đặc biệt khác. Bằng cách tra cứu các giá trị lượng giác tương ứng trong bảng, chúng ta có thể xác định các góc mà các hàm lượng giác có giá trị cần tìm, từ đó giải được phương trình một cách dễ dàng.

Những mối quan hệ của các hàm lượng giác hay các thuật toán lặp lại cũng được thể hiện rõ trong bảng phép tính lượng giác này. Ví dụ, ta có thể thấy rằng sin(x) = cos(90° – x) và cos(x) = sin(90° – x). Điều này cho phép chúng ta áp dụng các phép tính lượng giác khác nhau để tính toán các giá trị tương đương và tận dụng các tính chất đối xứng của các hàm lượng giác.
Vật lý
Trong lĩnh vực vật lý, các công thức lượng giác đóng một vai trò cực kỳ quan trọng trong việc tính toán và mô hình hóa các hiện tượng liên quan đến sóng, các dao động và các hiệu ứng giao thoa. Các phép tính lượng giác cho phép chúng ta xác định các thông số quan trọng như biên độ, tần số, chu kỳ và pha của các sóng âm, sóng sáng và các hiện tượng dao động khác. Ví dụ, khi ta muốn tính toán biên độ của một sóng âm, ta có thể sử dụng phép tính lượng giác để kết hợp các thông số như biên độ tối đa, góc pha và tần số. Từ đó, chúng ta có thể đưa ra mô hình chính xác cho sóng âm và dự đoán biên độ của nó tại các vị trí và thời điểm khác nhau.

Tương tự, trong trường hợp của sóng sáng, các phép tính lượng giác cho phép chúng ta tính toán các thông số như amplitud, bước sóng, góc pha và tốc độ truyền của sóng. Các công thức này cho phép chúng ta hiểu rõ hơn về tính chất sóng sáng và quan hệ giữa các thông số quan trọng này. Bên cạnh đó, các phép tính lượng giác cũng được sử dụng để giải quyết các bài toán liên quan đến hiệu ứng giao thoa, như hiệu ứng Interference và Diffraction. Nhờ vào các công thức này, chúng ta có thể tính toán và dự đoán sự tương tác và phân bố của các sóng trong các mô hình giao thoa phức tạp.
Kỹ thuật
Trong lĩnh vực điện tử, phép tính lượng giác được sử dụng để tính toán các giá trị điện áp, dòng điện và điện trở theo thời gian. Ví dụ, khi thiết kế mạch điện, chúng ta cần tính toán các thông số như biên độ, tần số, pha và hệ số công suất của các tín hiệu điện. Bảng phép tính lượng giác cung cấp các công thức quan trọng để tính toán các giá trị này và đưa ra các dự đoán chính xác về hiệu suất và hoạt động của mạch điện.

Trong lĩnh vực cơ khí, phép tính lượng giác cũng được sử dụng để tính toán và mô phỏng các hiện tượng dao động và chuyển động trong các hệ thống cơ khí. Ví dụ, trong thiết kế các cơ cấu chuyển động, chúng ta cần tính toán các thông số như biên độ, tốc độ, gia tốc và pha của các chuyển động dao động. Phép tính lượng giác giúp chúng ta hiểu và dự đoán chính xác các đặc tính và đường cong chuyển động của các hệ thống cơ khí.
Trong lĩnh vực xây dựng, phép tính lượng giác được sử dụng để tính toán và đo lường các thông số liên quan đến các công trình và cấu trúc. Ví dụ, trong tính toán và thiết kế các cấu trúc như tòa nhà và hệ thống, chúng ta cần tính toán các thông số như cường độ và biên độ của các dao động đất, chuyển động sóng và tải trọng động. Công thức lượng giác đóng vai trò quan trọng để tính toán các giá trị này và đưa ra các dự báo và phân tích về độ bền và an toàn của các công trình xây dựng.
Hình học
Công thức lượng giác đầy đủ không chỉ được áp dụng trong vật lý và các lĩnh vực kỹ thuật, mà còn có ứng dụng quan trọng trong hình học. Ví dụ, khi tính toán diện tích một tam giác, các phép tính lượng giác như Định lý Pythagoras, định lý sin và định lý cosin cho phép chúng ta tính toán các đại lượng này dựa trên thông tin đã biết về tam giác, ví dụ như độ dài hai cạnh và góc giữa chúng. Từ đó, chúng ta có thể tính toán diện tích của tam giác theo công thức diện tích tam giác: diện tích = 1/2 × cạnh a × cạnh b × sin(góc).

Ngoài ra, phép tính lượng giác cũng được áp dụng để tính toán các đại lượng hình học khác, như độ dài cạnh, chu vi và thể tích của các hình dạng phức tạp hơn như hình cầu, hình trụ, hình nón và hình hộp. Với sự ứng dụng của các phép tính lượng giác, chúng ta có thể tính toán các đại lượng này dựa trên thông tin về kích thước và hình dạng của các hình học.
Có những vấn đề cần lưu ý khi sử dụng bảng công thức lượng giác đầy đủ không?
Khi sử dụng bảng phép tính lượng giác đầy đủ, để đảm bảo tính chính xác và hiệu quả thì có một số vấn đề cần lưu ý như sau:
- Đọc và hiểu công thức: Trước khi áp dụng công thức, hãy đọc kỹ và hiểu ý nghĩa của từng công thức trong bảng lượng giác đầy đủ. Điều này giúp bạn áp dụng công thức chính xác và tránh sai sót do những nhận định thiếu thông tin.
- Xác định đơn vị góc: Kiểm tra xem bảng lượng giác sử dụng đơn vị góc nào. Thông thường, góc được đo bằng radian trong các công thức lượng giác. Nếu bạn có các giá trị góc được đo bằng độ, trước khi sử dụng công thức hãy chuyển đổi chúng sang radian.
- Kiểm tra giới hạn áp dụng: Hãy chú ý kiểm tra xem liệu các công thức mà bạn đang giữ có giới hạn áp dụng hay không. Trong nhiều trường hợp tính toán, chỉ có những phạm vi cụ thể của góc mới áp dụng được một số công thức cụ thể, ví dụ như các phép tính lượng giác ngược.
- Chọn công thức phù hợp: Có nhiều công thức khác nhau trong bảng phép tính lượng giác, do đó hãy đọc kỹ yêu cầu của bài toán để lựa chọn được công thức phù hợp, tránh mất thời gian khi phải làm đi làm lại do áp dụng sai công thức.
- Kiểm tra kết quả: Khi áp dụng công thức và ra được kết quả, đừng vội nộp bài ngay mà hãy dùng máy tính hoặc bảng lượng giác để so sánh kết quả của bạn và đảm bảo rằng nó nhất quán với dự đoán hoặc kết quả trước đó.

Tạm kết
Bảng công thức lượng giác mà tuyengiaothudo.vn đã tổng hợp trong bài viết này không chỉ là một tài liệu học thuật, mà còn là một công cụ quan trọng trong nhiều lĩnh vực ứng dụng. Từ vật lý và kỹ thuật đến công nghệ thông tin và nghệ thuật đồ họa, phép tính lượng giác được tích hợp rộng rãi trong các lĩnh vực này, giúp giải quyết nhiều vấn đề phức tạp liên quan đến hình học không gian.
XEM THÊM:
Nguồn: https://tuyengiaothudo.vn
Danh mục: Khám phá