Tâm của một tam giác là một khái niệm cơ bản nhưng cực kỳ quan trọng trong lĩnh vực hình học. Nó không chỉ là một điểm giữa đơn giản của một tam giác, mà còn là một vị trí chứa nhiều tính chất đặc biệt. Chúng cũng đóng vai trò quan trọng trong nhiều lĩnh vực khác nhau như kiến trúc, thiết kế và thậm chí trong nghiên cứu các định luật chuyển động của vũ trụ. Vì vậy, về bản chất Trọng tâm là gì?? Bản chất của điểm này là gì và làm thế nào để xác định nó? Hãy tham khảo thêm các gợi ý từ tuyengiaothudo.vn để có cái nhìn chi tiết hơn về chủ đề trên.
Trọng tâm là gì?
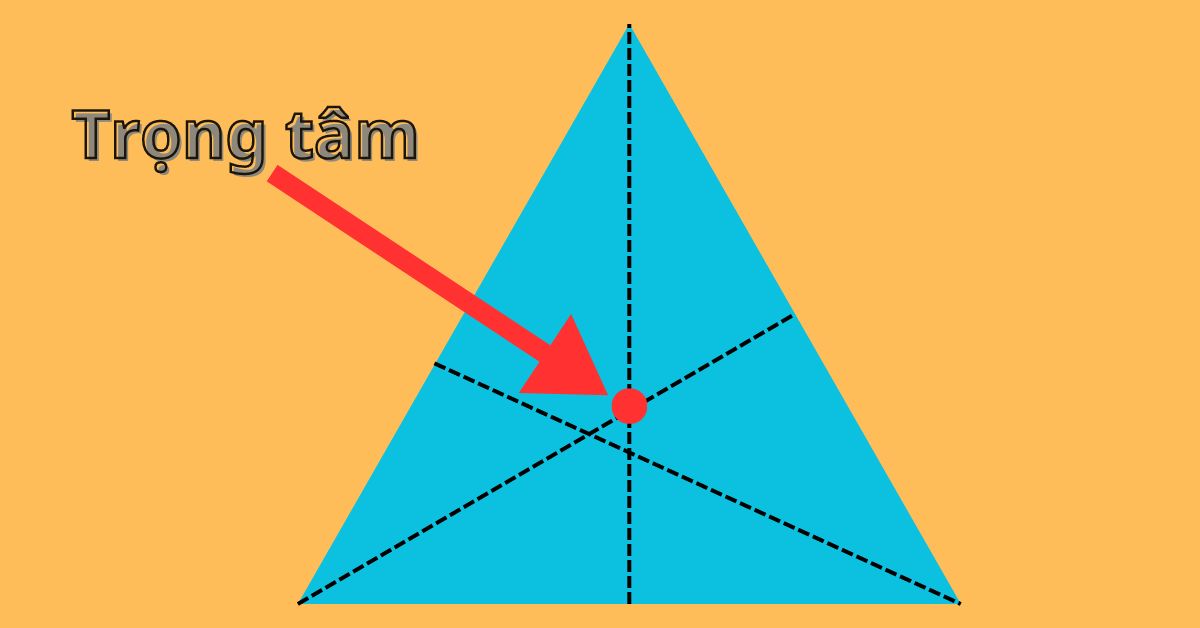
Trọng tâm của một hình học, đặc biệt là một hình tam giác, là một điểm trong không gian được tính toán dựa trên các tính chất hình học của hình đó. Đối với một hình tam giác, trọng tâm là giao điểm của các đường trung tuyến. Theo đó, các đường trung tuyến là các đoạn thẳng nối mỗi đỉnh của tam giác với điểm giữa của cạnh đối diện. Do đó, chúng ta sẽ có ba đường trung tuyến trong một hình tam giác và trọng tâm là điểm gặp nhau của ba đường trung tuyến này.
Bạn đang xem: Tính chất của trọng tâm và cách xác định trọng tâm tam giác trong Hình học

Về cơ bản, khi tìm hiểu về trọng tâm, nhiều người sẽ không biết rằng giao điểm của 3 đường trung tuyến trong một tam giác sẽ sở hữu nhiều tính chất đặc biệt. Chúng không chỉ quan trọng trong lĩnh vực hình học mà còn có ảnh hưởng sâu sắc đến nhiều lĩnh vực khác nhau như toán học thuần túy, vật lý, kỹ thuật, kiến trúc và thậm chí trong nghiên cứu về động lực học hành tinh.
Ngoài ra, trọng tâm cũng thường được sử dụng như một công cụ quan trọng để hiểu và giải quyết nhiều bài toán hình học phức tạp. Do đó, nếu bạn đang có nhiều thắc mắc về các tính chất và cách xác định điểm đặc biệt này trong một tam giác, bạn nên tham khảo nội dung được trình bày dưới đây.
Bản chất của trọng tâm là gì?
Hiểu được trọng tâm là gì, tuy nhiên, trên thực tế, ít ai nắm bắt được đầy đủ các tính chất của điểm đặc biệt này. Hiểu được nhu cầu đó, chúng tôi đã biên soạn một số tính chất cơ bản của trọng tâm trong tam giác để bạn có thể xem lại qua nội dung sau:
- Điểm giữa của các cạnh: Tâm là trung điểm của mỗi cạnh của tam giác. Điều này có nghĩa là khoảng cách từ tâm đến mỗi đỉnh bằng nhau và cũng bằng một nửa chiều dài của cạnh tương ứng.
- Giao điểm của các đường trung tuyến: Tâm là giao điểm của ba đường trung tuyến của một tam giác. Điều này có nghĩa là từ tâm, bạn có thể vẽ ba đường thẳng nối ba điểm giữa của tam giác để tạo thành ba đường trung tuyến. Đồng thời, giao điểm của ba đường trung tuyến được gọi là tâm.
- Tâm đối xứng: Tâm được gọi là tâm đối xứng của một tam giác. Nói một cách đơn giản, nếu bạn vẽ một đường thẳng từ tâm đến một đỉnh, nó sẽ chia tam giác thành hai phần bằng nhau.
- Tâm cân của tam giác đều:Trong một tam giác đều, tâm là tâm cân, nghĩa là nó cách đều mỗi đỉnh và cũng là giao điểm của ba đường trung tuyến.

Trọng tâm của các tam giác đặc biệt
Trong các bài toán, chúng ta thường gặp nhiều bài toán đòi hỏi phải xác định trọng tâm của các tam giác như: tam giác vuông, tam giác cân, tam giác đều,… Trong mỗi tam giác này, trọng tâm sẽ biểu diễn một tính chất khác nhau. Đồng thời, chúng cũng biểu diễn một giá trị đặc biệt mà bạn có thể tham khảo chi tiết ở nội dung bên dưới.
Tâm trong tam giác vuông
Trọng tâm trong tam giác vuông là gì? Đó là một điểm có những tính chất rất đặc biệt. Để hiểu rõ hơn về điều này, chúng ta hãy cùng xem xét các gợi ý về tính chất của trọng tâm trong tam giác vuông như sau:
- Tâm của tam giác vuông cũng là tâm đối xứng của tam giác. Chúng cũng là trung điểm của cạnh đối diện với góc vuông. Điều này có nghĩa là nếu bạn vẽ một đường thẳng từ tâm đến góc vuông, nó sẽ chia cạnh đối diện thành hai phần bằng nhau.
- Vì tam giác vuông có một góc vuông và một góc 45 độ, nên tâm cũng là điểm giữa của cạnh huyền (cạnh chứa góc vuông). Điều này tạo ra một tính chất đặc biệt là tâm và điểm giữa của cạnh huyền là cùng một điểm.

Trọng tâm trong tam giác cân
Dựa trên tính chất của trọng tâm, trọng tâm của tam giác cân cũng có những tính chất đặc biệt sau:
- Tâm là điểm giữa của cạnh đối diện với đỉnh của tam giác cân. Điều này có nghĩa là khoảng cách từ tâm đến mỗi đỉnh của tam giác là bằng nhau.
- Vì tam giác cân đối xứng trục với đường trung tuyến, nên tâm của tam giác này cũng là giao điểm của ba đường trung tuyến. Mỗi đoạn thẳng từ tâm đến một đỉnh của tam giác cân được gọi là đường trung tuyến.
- Tâm cũng là tâm đối xứng của tam giác cân, nghĩa là nếu bạn vẽ một đường thẳng từ tâm đến một đỉnh, nó sẽ chia tam giác thành hai phần bằng nhau.

Trọng tâm của tam giác đều
Tương tự như tính chất của trọng tâm trong tam giác đều, trong tam giác đều, điểm đặc biệt cũng sở hữu một số tính chất quan trọng sau:
- Tâm là giao điểm của ba đường trung tuyến của một tam giác đều. Các đường trung tuyến này cũng là các đoạn thẳng nối tâm với các đỉnh tương ứng. Do đó, tâm của một tam giác đều trùng với trung điểm của các đỉnh của tam giác. Điều này có nghĩa là khoảng cách từ tâm đến mỗi đỉnh của tam giác là bằng nhau.
- Tâm là tâm đối xứng của một tam giác đều. Nếu bạn vẽ một đường thẳng từ tâm đến một đỉnh, nó sẽ chia tam giác thành hai phần bằng nhau.
- Các góc và cạnh của tam giác trọng tâm đều bằng nhau về độ dài và độ lớn. Do đó, trọng tâm trong tam giác đều cũng được coi là điểm biểu diễn tâm đường tròn trong các bài toán.

Cách xác định chính xác trọng tâm trong tam giác
Sau khi hiểu được bản chất và khái niệm về trọng tâm, để xác định chính xác điểm đặc biệt này, bạn nên áp dụng 2 phương pháp sau.
Phương pháp 1: Sử dụng công thức toán học
Trong hình học tam giác, việc xác định trọng tâm là một phép toán cực kỳ quan trọng để bạn có thể giải quyết các bài toán. Để xác định trọng tâm của một tam giác, việc sử dụng công thức toán học là điều bạn không nên bỏ qua. Theo phương pháp đó, bạn có thể giả sử rằng trọng tâm G của tam giác ABC có tọa độ (xG;yG) có thể xác định một cách đơn giản. Trước tiên, chúng ta tính tọa độ trung bình của các đỉnh tam giác: xG = xA + xB + xC3 và yG = yA + yB + yC3. Công thức này có nghĩa là trọng tâm nằm ở tâm khối lượng của tam giác, chịu ảnh hưởng như nhau từ cả ba đỉnh.

Ngoài ra, để xác định trọng tâm bằng công thức toán học, chúng ta cũng có thể nắm bắt được một tính chất quan trọng khác. Trọng tâm cũng là giao điểm của ba đường trung tuyến trong tam giác ABC. Trong đó, mỗi đỉnh A, B và C được nối với trọng tâm G thông qua đường trung tuyến tương ứng của nó. Điều này tạo ra một điểm G đặc biệt. Đây là nơi các đường trung tuyến gặp nhau. Để xác định tọa độ chính xác của G, chúng ta có thể giải hệ phương trình của ba đường trung tuyến này.
Phương pháp 2: Sử dụng công cụ hình học
Xem thêm : Các cách làm thiệp bằng giấy A4 đơn giản, dễ làm, ý nghĩa
Một phương pháp truyền thống không thể bỏ qua khi xác định tâm là sử dụng thước kẻ và compa. Theo cách này, bạn có thể dễ dàng đo chiều dài các cạnh của tam giác và từ đó xác định trung điểm của chúng. Đầu tiên, sử dụng thước kẻ để đo chiều dài cạnh của tam giác. Sau đó, vẽ một đường thẳng qua trung điểm của cạnh đó bằng compa. Lặp lại quy trình này cho cả ba cạnh của tam giác. Tâm sẽ là điểm mà cả ba đường thẳng giao nhau, đảm bảo tính nhất quán giữa các đường trung tuyến và độ chính xác của tâm.

Ngoài ra, chúng ta cũng có thể áp dụng công nghệ để tính trọng tâm của một tam giác. Bằng cách sử dụng phần mềm đồ họa hoặc các công cụ tính toán, người dùng chỉ cần nhập tọa độ của ba đỉnh của tam giác. Các phần mềm này sẽ tự động thực hiện quá trình tính toán phức tạp, đưa ra tọa độ chính xác của trọng tâm. Điều này không chỉ tiết kiệm thời gian mà còn giảm nguy cơ sai sót trong quá trình đo lường và tính toán, đặc biệt là khi các tam giác có hình dạng phức tạp và khiến việc xác định trọng tâm trong tam giác của bạn trở nên khó khăn.
Các bài toán ví dụ liên quan đến tính chất trọng tâm của tam giác
Đề tài: Cho một tam giác có các đỉnh A, B, C. Tam giác này có đường trung tuyến AD bằng 9 cm. Trọng tâm là gì và đoạn thẳng AI dài bao nhiêu?

Câu trả lời: Theo đề bài, ta sẽ kẻ thêm một đường trung tuyến nữa từ đỉnh B cắt cạnh AC. Giao điểm ta sẽ giả sử là E. Do đó, ta sẽ có thêm một đường trung tuyến nữa là BE. Trong đó, giao điểm của hai đường trung tuyến chính là trọng tâm của tam giác này (gọi là I).
Theo tính chất cơ bản nhất của đường trung tuyến, “Đường trung tuyến sẽ bằng ⅔ độ dài từ đỉnh đến trọng tâm của góc”. Do đó, ta có AD = 9cm => AI = ⅔ x 9 = 6 cm. Do đó, đáp án cần tìm cho bài toán trên là AI dài 6cm.
Nhìn chung, bài viết hôm nay tuyengiaothudo.vn cũng được trình bày rõ ràng về Trọng tâm là gì? và các tính chất đặc biệt của điểm này trong tam giác. Hy vọng với giải pháp trên, các em sẽ nắm được cách xác định trọng tâm và hoàn thành các bài toán hình học cơ bản trên lớp. Chúc các em đạt thành tích xuất sắc trong học kỳ này.
XEM THÊM
Nguồn: https://tuyengiaothudo.vn
Danh mục: Khám phá