Thể tích hình chóp là kiến thức cơ bản mà học sinh lớp 12 cần nắm vững để học tốt môn Hình học. Các bài toán về hình chóp cũng xuất hiện rất nhiều trong các kỳ thi THPT Quốc gia nên các em cần học tập thật kỹ và làm bài tập thường xuyên để nắm vững kiến thức. Bài viết dưới đây sẽ chia sẻ thêm về hình chóp và công thức tính nhanh thể tích của chúng.
Khái niệm về kim tự tháp và một số tính chất
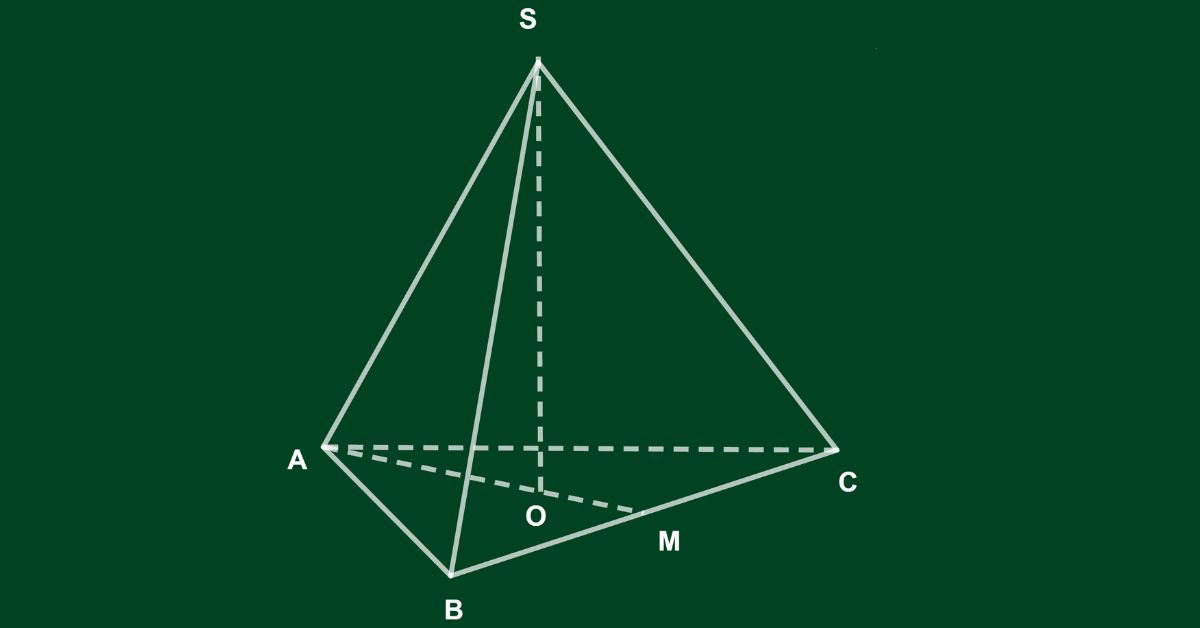
Trước khi tìm hiểu về thể tích của một kim tự tháp, mọi người cần tìm hiểu về kim tự tháp. Đây là một hình dạng hình học bao gồm một đáy đa giác với các tam giác đều có chung một đỉnh. Đây cũng là đỉnh của kim tự tháp. Chiều cao trong một kim tự tháp là một đường thẳng có thể đi qua đỉnh và tạo thành một góc vuông với đáy.
Bạn đang xem: Công thức tính nhanh thể tích khối chóp – Tính toán dễ dàng và hiệu quả

Hiện nay, có hai dạng kim tự tháp phổ biến và tên của chúng phụ thuộc vào hình dạng của mặt phẳng đáy. Đó là kim tự tháp tứ giác và kim tự tháp tam giác. Ngoài ra, kim tự tháp có một số tính chất mà bạn cần biết như sau:
- Một kim tự tháp có các cạnh bằng nhau có đáy bằng chiều cao của kim tự tháp nằm ở tâm của đường tròn ngoại tiếp đa giác đáy.
- Một kim tự tháp gồm các mặt bên được đặt ở cùng một góc với đáy, khi đó chiều cao của đáy kim tự tháp chính là tâm của đường tròn nội tiếp đa giác đáy.
- Hình chóp gồm một mặt bên tạo thành góc vuông với mặt đáy, khi đó chân chiều cao của hình chóp là chân đường vuông góc kẻ từ đỉnh hình chóp xuống cạnh đáy của mặt bên này.
- Nếu hai mặt bên của một hình chóp vuông góc với đáy thì giao tuyến của hai mặt bên này cũng vuông góc với đáy.
Công thức được sử dụng để tính nhanh thể tích của một kim tự tháp
Thể tích của kim tự tháp bây giờ có thể được tính toán nhanh chóng bằng công thức:
V = 1/3 x S x H.
Trong đó:
- S: Diện tích mặt phẳng đáy
- h: Chiều cao của kim tự tháp.

Một số dạng tính toán thể tích kim tự tháp phổ biến và bài tập ứng dụng
Hiện nay, có rất nhiều dạng toán liên quan đến tính thể tích hình chóp vì đây là một dạng hình học đặc biệt. Sau đây là một số dạng toán thường gặp để tính thể tích hình chóp cùng với các bài tập liên quan. Học sinh có thể tham khảo:
Công thức toán học để tính hình chóp V có các mặt bên ⊥ có đáy
Để nhận biết dạng bài toán tính thể tích này, bạn cần xem xét cẩn thận hình chóp mà bài toán đưa ra. Nếu hình chóp có 2 mặt bên ⊥ với mặt đáy và chiều cao của hình chóp cũng là giao điểm của 2 mặt bên đó, ta sẽ áp dụng công thức giải này.
Để tính chiều cao của kim tự tháp, hãy sử dụng định lý sau:
Để hiểu rõ hơn cách tính V của hình chóp này, vui lòng xem bài tập minh họa sau: Cho hình chóp S.ABCD có mặt đáy là tam giác vuông ABC tại B, một mặt phẳng có tên là SBC ⊥ với một mặt phẳng có tên là ABC, BC = 4a, BA = 3a. Cho góc SBC bằng 30 độ và SB bằng 2a√3. Tính thể tích của hình chóp S.ABC.

Trả lời:
Vẽ đường thẳng SH sao cho ⊥ trùng với BC (H phải nằm trên cạnh BC). Khi đó ta có:
- Mặt phẳng SBC ⊥ với mặt phẳng ABC
- BC là giao tuyến của mặt phẳng SBC với mặt phẳng ABC
- SH vuông góc với BC
- SH nằm trong mặt phẳng SBC
→ SH vuông góc với mặt phẳng ABC
Tiếp theo, chúng ta xét tam giác SHB vuông tại H, ta có:
- SH = SB x sin của góc SBC = 2a√3 x sin30 = a√3
- Diện tích tam giác ABC = 1/2 x BA x BC = 1/2 x 3a x 4a = 6a^2
- Thể tích của hình chóp S.ABC = 1/3 x SH x Diện tích tam giác ABC = 1/3 xa√3 x 6a^2 = 2a^3√3
Công thức toán học để tính hình chóp V có cạnh bên ⊥ và đáy
Như đã đề cập ở trên, công thức tính V của một kim tự tháp là ⅓ S x h. Vì kim tự tháp cũng có một cạnh bên ⊥ với mặt phẳng đáy, nên có thể suy ra rằng cạnh bên này là chiều cao của kim tự tháp với h bằng chiều dài của cạnh bên ⊥ với đáy. Bạn có thể hiểu rõ hơn về loại tính toán này cho V của một kim tự tháp thông qua bài tập sau:
Bài tập: Cho hình chóp S.ABC có cạnh SA ⊥ vuông góc với đáy, độ dài SA là 4, độ dài AB là 6, độ dài BC là 10 và độ dài CA là 8. Hãy tính V của hình chóp S.ABC?

Trả lời:
Ta có AB^2 + AC^2 = 6^2 + 8^2 = BC^2
→ Tam giác ABC vuông tại A.
Vậy diện tích của tam giác này là: S = 1/2 AB x AC = 1/2 x 6 x 8 = 24
Vậy thể tích của hình chóp S.ABC = 1/3 x SA x S của tam giác ABC = 1/3 x 4 x 24 = 32
Bài toán V của hình chóp S.ABCD có đáy là hình vuông
Xem thêm : Tổng hợp kinh nghiệm chọn balo latop, các thương hiệu được ưa chuộng
Đối với kim tự tháp có đáy hình vuông, bạn có thể thực hiện các bài tập sau:
Bài tập: Cho hình chóp S.ABCD có mặt đáy là hình vuông cạnh a, cạnh SC tạo với mặt phẳng SAB một góc 30 độ, cạnh SA ⊥ với đáy. Tính V của hình chóp này?

Trả lời:
- Vì mặt phẳng ABCD là hình vuông nên ta có cạnh BC vuông góc với cạnh AB (1).
- Nhưng cạnh SA vuông góc với mặt phẳng ABCD, do đó có thể suy ra cạnh SA vuông góc với BC (2).
- Từ (1) và (2), ta suy ra cạnh BC cũng vuông góc với mặt phẳng SAB.
- Do đó, góc tạo bởi cạnh SA và mặt phẳng SAB = Góc tạo bởi cạnh SC và SB = Góc CSB = 30 độ.
- Từ đó ta có thể suy ra BC/SB = tan30 = √3/3
- → SB = √3BC = √3a
- Dựa trên định lý Pythagore, cạnh SA = √SB^2 – AB^2 = √3a^2 – a^2 = √2a
Do đó, thể tích của hình chóp S.ABCD là: 1/3 x SA x S của hình vuông ABCD = 1/3 √axa^2 = (√2/3) xa^3
Công thức toán học để tính thể tích của một hình chóp lập phương
Đây là một kim tự tháp rất đặc biệt vì tất cả các mặt của kim tự tháp đều là hình lập phương. Do đó, tính V của kim tự tháp hình lập phương này rất dễ: V = axaxa = a^3. Sau đây là một bài tập minh họa:
Cho một hình chóp lập phương có đường chéo dài 27cm. Tính V của hình chóp này?

Trả lời:
Chiều dài các cạnh của hình chóp trên là 27/√3 (cm).
Vậy V của khối chóp lập phương này là V = (27/√3)^3 = 6561/√3 (cm^3).
Dạng toán học tính V của lăng trụ chóp có đáy là tam giác đều
Nếu một hình chóp bao gồm các mặt bên hình bình hành và hai đáy song song có kích thước bằng nhau, thì nó được coi là một hình chóp lăng trụ. Nếu hình chóp lăng trụ này bao gồm các đáy là các tam giác đều, thì nó là một hình chóp lăng trụ tam giác đều. Sau đây là một số bài tập giúp bạn hiểu rõ hơn.
Bài tập: Cho một lăng trụ đứng ABC.A’B’C’ có mặt đáy là tam giác đều ABC có cạnh a bằng 2cm và chiều cao h bằng 3cm. Hãy tính thể tích của khối chóp lăng trụ này?

Trả lời:
Vì đáy của hình chóp trên là tam giác đều cạnh a nên S của tam giác này là a^2 x √3/4 = 2^2 x (√3/4) = √3 (m2)
Từ đó ta có thể suy ra thể tích của lăng trụ này bằng S của tam giác ABC xh = √3 x 3= 3√3 (m3)
Công thức toán học để tính V của một hình chóp có đáy lục giác đều
Để hiểu rõ hơn về cách tính thể tích của kim tự tháp này, vui lòng xem bài tập sau:
Bài tập: Cho một hình chóp có đáy là lục giác đều, góc tạo bởi cạnh bên và mặt phẳng đáy bằng 30 độ, độ dài cạnh đáy là a. Tính V của hình chóp này?

Trả lời:
Ta gọi tên hình chóp trên là S.ABCDEF, gọi O là tâm mặt đáy ABCDEF.
Từ đó ta suy ra OA = OC = OB = OD = OF = OE = AB = CD = BC = DE = FA = EF = a
→ Tam giác OAB là tam giác có độ dài các cạnh bằng a.
→ Diện tích đáy ABCDEF gấp 6 lần diện tích tam giác OAB.
→ Diện tích đáy ABCDEF bằng (3.a^2.√3)/2
Xem thêm : Hệ thống nâng cấp vũ khí trong Demon’s Souls: Làm thế nào để tối ưu hóa sức mạnh
Ta có cạnh SO vuông góc với mặt đáy ABCDEF
→ Góc tạo bởi cạnh SA và đáy = Góc SAO = 30 độ
→ Cạnh SO = OA x tan30 = (a√3)/3
Vậy thể tích của hình chóp S.ABCDEF = 1/3 x Diện tích đáy ABCDEF x SO = 1/3 x (3.a^2√3)/2 x (a√3)/3 = (a^3)/2
Công thức toán học để tính kim tự tháp V có hai cạnh bằng nhau ⊥
Bạn có thể tham khảo bài tập sau để biết cách tính V của hình chóp có hai cạnh vuông góc:
Cho tứ diện S.ABC gồm các cạnh SA, SC, SB và một cặp cạnh vuông góc. Cho SB = 4a, SA = 3a, SC = 5a. Tính V của hình chóp này?

Trả lời:
Ta có cạnh SA vuông góc với cạnh SC, cạnh SA vuông góc với cạnh SB → Cạnh SA vuông góc với mặt phẳng SBC.
Từ đó ta suy ra diện tích hình chóp tứ diện S.ABC = 1/3 x SA x diện tích mặt phẳng SBC = 1/6 x SA x SB x SC = 1/6 x 3a x 4a x 5a = 10a^3
Công thức toán học để tính chuyển động quay của một kim tự tháp tròn
Công thức tính V của một hình chóp tròn quay
Công thức tính V của hình chóp xoay tương tự như công thức tính V của hình chóp cơ bản:
V = 1/3 B xh
= 1/3 x π xr^2 xhx 1/3 x B xh
= 1/3 x π xr^2 xh
Trong đó:
- B: Diện tích đáy hình nón
- r: Bán kính của mặt phẳng đáy hình nón
- h: Chiều cao của hình nón

Bài tập tính thể tích hình chóp xoay
Bài tập sau đây sẽ giúp bạn hiểu rõ hơn cách tính thể tích của hình chóp tròn ở trên:
Cho một hình nón có chiều cao 2√5 với một mặt phẳng đi qua đỉnh của hình nón và cắt hình nón này thành một mặt cắt ngang có tam giác đều với S của tam giác = 9√3. Tính V của hình chóp giới hạn bởi hình nón của bài toán.
Trả lời:
Ta có một tam giác được tạo thành từ mặt cắt ngang của tam giác ABC như hình dưới đây, điểm I được coi là trung điểm của cạnh BC, coi a là độ dài cạnh của tam giác ABC. Do đó, ta có:
(a^2√3)/4 = 9√3 → (3a^2)/4 = 27 → AI = a√3 = 3√3
→ OI = √AI^2 – AO^2 = √27 – 20 = √7
Bán kính đáy hình nón là R = OC = √OI^2 + IC^2 = √7 + 9 = 4
Vậy V của kim tự tháp ở trên là V = 1/3 x π x 4^2 x 2√5 = (32√5π)/3
Nội dung trên đã chia sẻ khá nhiều công thức tính thể tích hình chóp nhanh chóng để các bạn học thuộc. Hy vọng các bạn có thể giải toán nhanh hơn với các công thức và bài tập trên. Đây là kiến thức cơ bản để các bạn học tốt môn hình học ở trường phổ thông.
Xem các bài viết liên quan:
Nguồn: https://tuyengiaothudo.vn
Danh mục: Khám phá