Tất cả điều bạn cần biết về diện tích bề mặt hình hộp chữ nhật

Diện tích hình hộp chữ nhật Có vẻ như công thức này dễ áp dụng trong các bài toán. Tuy nhiên, trên thực tế, đây lại là một trong những nỗi sợ lớn nhất của nhiều học sinh. Tuy nhiên, để vượt qua các bài toán thuộc loại hình hình học không gian này, trước tiên người dùng phải nắm được định nghĩa, tính chất và công thức tính toán của chúng. Theo đó, bài viết tuyengiaothudo.vn Dưới đây chắc chắn sẽ là sự lựa chọn không thể thiếu mà bạn nên tham khảo trong vấn đề này.

Có thể bạn quan tâm

Về hộp chữ nhật

Như đã trình bày, để áp dụng thành công phương pháp tính diện tích hình lăng trụ đứng, trước tiên bạn phải nắm được định nghĩa và tính chất của hình học không gian này. Dưới đây là những gợi ý về vấn đề này mà bạn có thể tham khảo.

Bạn đang xem: Tất cả điều bạn cần biết về diện tích bề mặt hình hộp chữ nhật

Định nghĩa

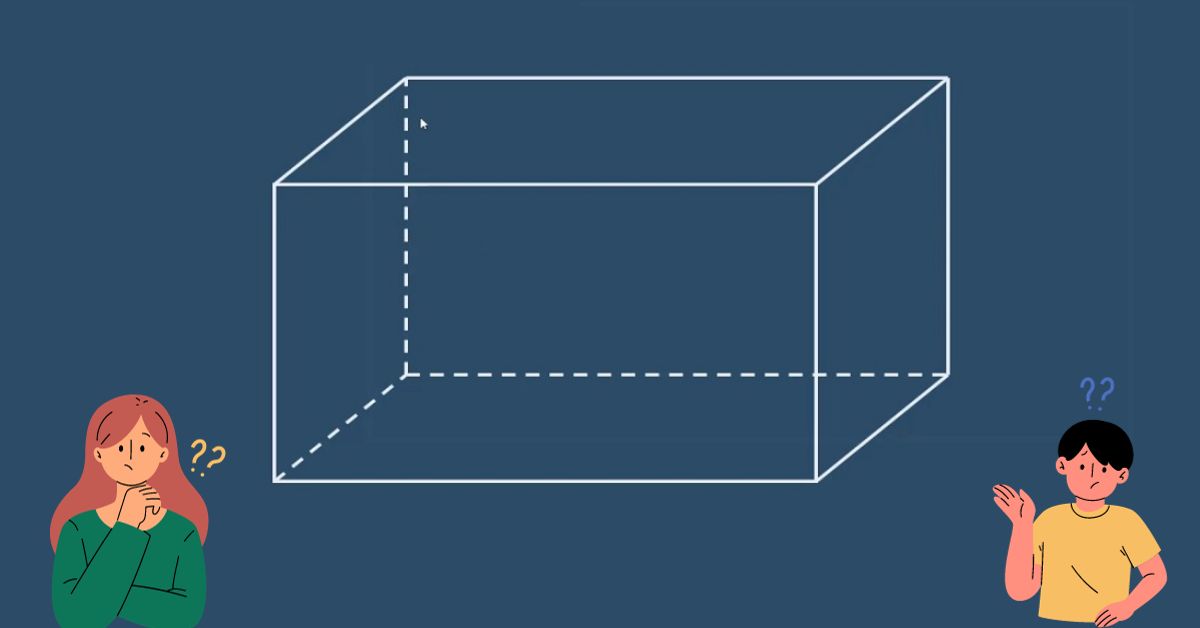
Lăng trụ chữ nhật là một hình học cơ bản và quen thuộc trong toán học. Cụ thể, đây là một loại lăng trụ có sáu cạnh, trong đó các cạnh đối diện song song và bằng nhau. Điều này tạo ra các góc vuông tại các giao điểm của các đường thẳng. Ví dụ, hộp phấn có thể là lăng trụ chữ nhật, mà bạn có thể thường xuyên gặp trong môi trường trường học.

Ngoài ra, bạn cũng có thể dễ dàng nhìn thấy hình hộp chữ nhật thường xuất hiện trong nhiều tình huống thực tế như bao bì sản phẩm, xây dựng, thiết kế nội thất và nhiều ứng dụng khác. Đặc biệt, công thức tính diện tích hình hộp chữ nhật không chỉ giúp người dùng hiểu được các hình khối hình học mà còn ứng dụng chúng vào nhiều bài toán thực tế, từ quy hoạch đô thị đến sản xuất, kỹ thuật. Điều này cho thấy tầm quan trọng và ảnh hưởng sâu sắc của hình học không gian này trong đời sống con người.

Thiên nhiên

Hình hộp chữ nhật là hình học không gian sở hữu nhiều tính chất đặc biệt mà bạn có thể tham khảo như:

Trong một lăng trụ đứng, hai mặt đối xứng sẽ luôn có S bằng nhau. Điều này là do chúng được tạo ra đối xứng và có các cạnh bằng nhau.
Không chỉ diện tích, chu vi của các mặt đối diện trong hình học đặc biệt này cũng bằng nhau. Tính chất này giúp người dùng dễ dàng tính toán chiều dài và diện tích của một lăng trụ chữ nhật.

Một lăng trụ chữ nhật có tổng cộng 12 cạnh, 6 mặt và 8 đỉnh. Tính chất này mang lại cho lăng trụ chữ nhật cấu trúc độc đáo và phức tạp. Nó cũng làm cho loại hình học này trở thành một đối tượng phổ biến được sử dụng trong nhiều lĩnh vực.
Đường chéo trong lăng trụ chữ nhật là các đoạn thẳng nối hai đỉnh không kề nhau. Chúng cắt nhau tại một điểm và tạo thành một kết nối đặc biệt giữa các mặt của lăng trụ.

Cách tính diện tích hình hộp chữ nhật chi tiết

Tính diện tích hình lăng trụ đứng không hề đơn giản như chúng ta nghĩ. Bởi vì công thức tính diện tích hình học này khá phức tạp và bao gồm nhiều thành phần cấu thành như diện tích xung quanh và diện tích đáy. Cụ thể, bạn có thể tham khảo hướng dẫn dưới đây để nắm được cách tính của chúng tôi.

Diện tích bề mặt của một hình hộp chữ nhật

Diện tích xung quanh (mặt) của một lăng trụ đứng chữ nhật là tổng diện tích của tất cả các mặt bên của lăng trụ (từ diện tích của hai đáy). Đối với một lăng trụ đứng chữ nhật, có bốn mặt bên có diện tích cần tính. Theo đó, ta sẽ giả sử chiều dài của lăng trụ này là a, chiều rộng là b và chiều cao là h, khi đó diện tích của mỗi mặt bên sẽ là ab (trong đó a là chiều dài và b là chiều rộng). Ngược lại, chu vi của mỗi mặt bên sẽ bằng 2 (a + b).

Vì vậy, chu vi của hình hộp chữ nhật sẽ được tính theo công thức sau:

Sxung quanh = 2 (a + b) xh

Tổng diện tích của một hình hộp chữ nhật

Tổng diện tích của một lăng trụ chữ nhật là tổng diện tích của tất cả các mặt của nó, bao gồm các mặt bên và đáy. Nói một cách đơn giản, đây là diện tích xung quanh và diện tích đáy của không gian hình học này. Theo đó, nếu chúng ta vẫn cho rằng chiều dài của lăng trụ này là a, chiều rộng là b và chiều cao là h, thì diện tích đáy sẽ bằng 2ab.

Từ đó, công thức tính diện tích hình lăng trụ đứng sẽ được trình bày chi tiết như sau:

Xem thêm : 0932 là mạng gì? Khám phá ý nghĩa đặc biệt của số 0932 chi tiết nhất

Stổng thể = Sđáy+ Sxung quanh = [2ab + 2 (a + b) x h]

Ví dụ về cách tính diện tích hình lăng trụ đứng

Để nắm bắt và thực hiện các công thức trên để tính S của hình hộp chữ nhật, chúng ta hãy thử một số dạng bài toán sau.

Ví dụ 1: Cơ bản

Đăng: Cho một hình hộp chữ nhật có chiều dài a = 20 cm, chiều rộng b = 7 cm và chiều cao h = 20 cm. Tính tất cả các diện tích của hình hộp chữ nhật theo công thức bạn đã học.

Câu trả lời:

Dựa vào dữ liệu đã cho, áp dụng công thức tính diện tích toàn phần hình hộp, ta sẽ có câu trả lời:

Diện tích xung quanh = 2 (a + b) xh = 2 (20 +7) x 20 = 540 cm2

Vậy diện tích toàn phần của hình hộp chữ nhật ta cần tìm sẽ là:

Tổng cộng = [2ab + 2 (a + b) x h] = [2 x 20 x 7 + 2 (20 +7) x 20] = 820 cm2

Trả lời: 820 cm2

Ví dụ 2: Nâng cao

Đề tài: Dựa vào công thức tính diện tích hình hộp chữ nhật đã học, hãy xác định chiều cao (h) và diện tích toàn phần của chúng. Giả sử hình hộp này có chiều dài a = 20 cm, chiều rộng b = 7 cm và diện tích toàn phần là 540 cm2. Hãy tính cụ thể Stp của hình hộp chữ nhật trên.

Câu trả lời:

Từ công thức tính diện tích xung quanh, ta có:

Xung quanh = 2 (a + b) xh => h = Xung quanh : [2 (a + b)] = 540 : [2 (20 + 7)] = 20cm

Xem thêm : Phim bl Thái Lan: Top 10 tựa phim hay nhất mà bạn nên thử

Như vậy, chiều cao cần thiết của hình hộp chữ nhật này là 20 cm. Do đó, Stp của hình hộp chữ nhật trên sẽ dễ dàng được áp dụng theo công thức sau:

Tổng cộng = [2ab + 2 (a + b) x h] = [2 x 20 x 7 + 2 (20 +7) x 20] = 820 cm2

Trả lời: 820 cm2

Những lưu ý khi tính diện tích hình hộp chữ nhật

Khi tính S của hình hộp chữ nhật, người dùng cần lưu ý một số điểm quan trọng để đảm bảo tính chính xác và hiểu bài toán như sau:

Để tính diện tích hình hộp chữ nhật, bạn cần xác định chính xác kích thước chiều dài (a), chiều rộng (b) và chiều cao (h) để tránh sai sót trong quá trình tính toán.
Đảm bảo tất cả các kích thước trong hộp văn bản được hiển thị theo cùng một đơn vị. Nếu các đơn vị khác nhau, hãy chuyển đổi chúng sang cùng một đơn vị trước khi tính toán.

Sau khi tính diện tích, hãy kiểm tra lại kết quả để đảm bảo độ chính xác. Đôi khi một lỗi nhỏ khi đọc số liệu hoặc thực hiện phép tính có thể dẫn đến kết quả không chính xác.
Hiểu bối cảnh và yêu cầu của bài toán. Điều này giúp xác định diện tích nào cần được tính toán (chu vi, tổng) và cách sử dụng kết quả tính toán trong bối cảnh cụ thể của bài toán.
Trong nhiều trường hợp dữ liệu quá lớn, bạn có thể sử dụng máy tính bỏ túi hoặc công cụ tính toán trực tuyến để giúp giảm lỗi tính toán và tăng độ chính xác trong quá trình giải.

Ứng dụng công thức tính diện tích hình hộp chữ nhật

Công thức tính diện tích hình lăng trụ đứng thực sự đóng vai trò đặc biệt trong nhiều lĩnh vực, đặc biệt là trong phương diện học tập. Sự xuất hiện liên tục trong các kỳ thi quốc gia khiến công thức này trở thành chủ đề được nhiều học sinh quan tâm. Điều này có tác động lớn đến chất lượng đào tạo trong ngành giáo dục. Đồng thời, trang bị cho học sinh những kỹ năng cần thiết trong việc tính toán và làm việc trong môi trường hình học đa chiều.

Ngoài ra, trong lĩnh vực xây dựng và kiến trúc, công thức này được sử dụng để tính toán lượng vật liệu cần thiết để xây dựng các công trình như tường, sàn và mái. Nó cũng giúp cung cấp báo giá và ước tính chi phí xây dựng. Nhiều người thậm chí còn áp dụng phương pháp tính diện tích hình hộp chữ nhật để xác định bề mặt của sản phẩm. Điều này giúp họ dễ dàng đưa ra quyết định về lượng vật liệu đóng gói cần sử dụng và thời gian hoàn thành công việc được giao.

Ngoài ra, công thức tính S của hình hộp chữ nhật cũng được ứng dụng trong nhiều lĩnh vực khác nhau. Chúng đóng vai trò quan trọng trong thiết kế đồ họa, bất động sản, quy hoạch đô thị,… Do đó, việc hiểu và áp dụng tính toán hình học không gian này là điều cần thiết để tất cả học sinh nắm bắt.

Những câu hỏi thường gặp khi tính diện tích hình hộp chữ nhật

Nếu bạn gặp vấn đề khi áp dụng công thức tính thể tích hình hộp chữ nhật, vui lòng tham khảo một số giải pháp được chúng tôi gợi ý bên dưới.

Khi nào ta phải tính diện tích toàn phần của một hình lăng trụ chữ nhật?

Hồi đáp: Trên thực tế, đối với các bài toán, học sinh nên tính diện tích của một lăng trụ đứng hình chữ nhật khi học về chiều dài, chiều rộng và chiều cao. Chi tiết hơn, người dùng nên tính Stp của một lăng trụ đứng hình chữ nhật khi bạn cần thông tin về tổng diện tích của tất cả các mặt bao gồm mặt dưới và mặt trên, cùng với tất cả các mặt bên của lăng trụ.

Mục đích của việc tính diện tích xung quanh của hình hộp chữ nhật là gì?

Hồi đáp:Thông thường, mục đích của việc tính diện tích bên là để đo diện tích bề mặt xung quanh một hộp chữ nhật. Điều này thường được sử dụng trong sơn, lót hoặc đóng gói để giúp ước tính lượng vật liệu cần thiết và chi phí liên quan mà không cần xem xét đến đáy và đỉnh của hộp chữ nhật.

Nói chung, công thức tính toán diện tích hình hộp chữ nhật được sử dụng rộng rãi trong cuộc sống của chúng ta. Do đó, tuyengiaothudo.vn Hy vọng rằng, sau khi nghiên cứu định nghĩa, tính chất và công thức của hình học này, bạn đọc có thể áp dụng vào công việc và học tập của mình. Đừng quên cập nhật những gợi ý bên dưới để bổ sung vào kho kiến thức cá nhân của bạn.

XEM THÊM

Nguồn: https://tuyengiaothudo.vn
Danh mục: Khám phá