Chu vi hình thoi là kiến thức cơ bản mà học sinh và mọi người phải nắm vững vì nó xuất hiện trong nhiều dạng bài tập hình học và ứng dụng trong cuộc sống. Nếu bạn chưa biết về hình học này và chưa biết cách tính diện tích và chu vi của nó thì hãy theo dõi bài viết sau đây. Bài viết sẽ chia sẻ một số kiến thức về hình thoi và các bài tập xoay quanh hình này.
Hình thoi là dạng hình học gì?
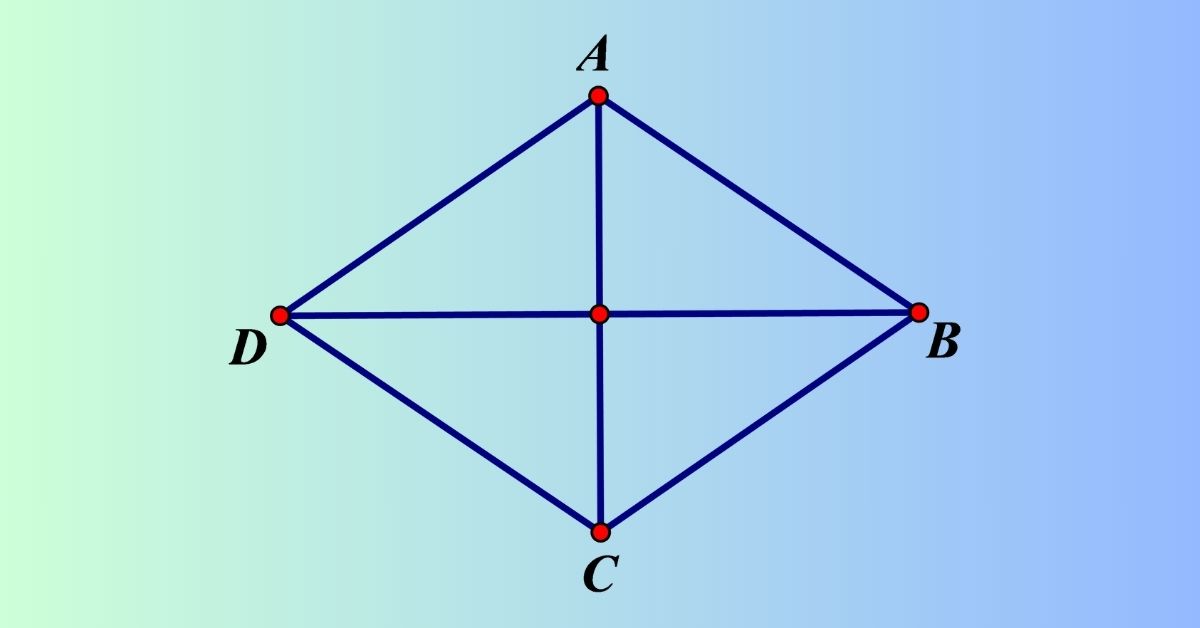
Hình thoi là một hình học có bốn cạnh bằng nhau. Nhiều người cũng coi hình thoi là hình bình hành có hai cạnh kề bằng nhau và hai đường chéo trong hình này cũng cắt nhau tại điểm giữa của mỗi đường thẳng và vuông góc với nhau.
Bạn đang xem: 21 công thức tính chu vi và diện tích hình thoi để giúp bạn hiểu rõ hơn

Nếu một hình thoi có 4 góc vuông bên trong có cùng số độ thì nó được coi là hình vuông. Do đó, một hình thoi có một hình dạng hình học đặc biệt được gọi là hình vuông, nó có 4 góc vuông và 4 cạnh có cùng độ dài. Tất cả các hình vuông đều được coi là hình thoi, nhưng không phải tất cả các hình thoi đều được coi là hình vuông.
Hình thoi có tính chất gì?
Trước khi tìm hiểu về chu vi của hình thoi, mọi người cần tìm hiểu hình học này có những tính chất gì. Sau đây là một số tính chất của hình thoi:

- Hình thoi có tất cả các tính chất của hình bình hành. Ví dụ, nó có các cạnh đối bằng nhau và song song, nó có các góc đối bằng nhau có cùng số độ và hai đường chéo trong hình cắt nhau tại trung điểm của chúng.
- Hình thoi gồm các góc đối nhau có cùng số độ, tổng các góc của một hình thoi = 360 độ.
- Hình thoi gồm hai đường chéo cắt nhau tại trung điểm và vuông góc với nhau.
- Hình thoi gồm hai đường chéo được coi là đường phân giác của tất cả các góc của hình thoi.
Công thức tính chu vi hình thoi là gì?
Để tính chu vi của hình thoi, ta cần lấy tổng độ dài tất cả các cạnh hoặc lấy độ dài một cạnh rồi nhân với 4. Như vậy, ta có công thức tính chu vi như sau:
P = a + a + a + a
= rìu 4
Xem thêm : ViewSonic ra mắt màn hình 4K 27 inch mới với độ sáng 400 nits, giá từ 5 triệu đồng
Trong đó:
- P: Chu vi của hình thoi
- a: Độ dài các cạnh của hình thoi

Chúng tôi có ví dụ minh họa sau đây để giúp bạn hiểu rõ hơn về công thức trên:
Cho hình thoi có tên là ABCD và độ dài tất cả các cạnh = 4cm. Chu vi của hình thoi này là bao nhiêu?
Trả lời:
- Theo bài toán, cạnh của hình thoi là a = 4cm
- Vậy chu vi của hình này là: 4 x 4 = 16 (cm)
Công thức tính diện tích hình thoi là gì?
Ngoài việc tìm hiểu về chu vi hình thoi, bạn nên tìm hiểu thêm về cách tính diện tích của hình này. Diện tích hình thoi sẽ bằng một nửa tích độ dài hai đường chéo. Trong hình thoi, đường chéo là đường thẳng dùng để nối hai đỉnh đối diện. Từ đó, ta có cách tính diện tích hình thoi theo công thức sau:
S = 1/2 x (d1 x d2)
Xem thêm : ViewSonic ra mắt màn hình 4K 27 inch mới với độ sáng 400 nits, giá từ 5 triệu đồng
Trong đó:
- S: Diện tích hình thoi
- d1: Đường chéo số 1
- d2: Đường chéo số 2

Để hiểu rõ hơn về công thức tính diện tích này, vui lòng xem ví dụ sau:
Cho hình thoi ABCD có độ dài hai đường chéo là 6cm và 10cm. Tính S của hình thoi này?
Trả lời:
S của hình thoi trên = (6 x 10) / 2 = 30cm2
Ngoài phương pháp tính S của hình thoi nêu trên, hiện nay còn có nhiều cách tính S của hình thoi như sau:
Tính hình thoi S bằng công thức tam giác
Nếu bạn biết số đo góc của hình thoi, bạn có thể sử dụng công thức tam giác để tính S của hình thoi bằng công thức sau:
S = a^2 x sin A = a^2 x sin B = a^2 x sin C = a^2 x sin D
Ví dụ minh họa: Cho hình thoi ABCD có cạnh = 4cm và góc A = 30 độ. Tính S của hình thoi này?

Trả lời:
Phép tính 1:
S của hình thoi trên = a^2 x sin A = 16 x sin 30 độ = 8cm2
Phép tính 2:
- Vì ABCD được coi là hình thoi → Các tam giác được tạo thành từ hình thoi này đều là tam giác cân.
- Cho điểm O là giao điểm của hai đường chéo BD và AC. Do đó điểm O cũng được coi là trung điểm của hai đường chéo BD và AC. Do đó, BD cũng vuông góc với AO. Do đó, góc BAO bằng một nửa góc BAD và bằng 15 độ.
- Vậy cạnh AO = AB x góc cos BAO = 4 x cos15 độ = 3,84 cm
- Sau đó, ta sử dụng định lý Pythagoras trong tam giác có tên là AOB và có: AB² = OB² + AO². Từ đó ta suy ra OB² = AB² – AO² = 16 – 3,84² = 1,25. Do đó OB bằng 1,1 cm
- Vậy cạnh AC là 2, cạnh AO = 2 x 3,84 = 7,68cm và cạnh BD là 2 và cạnh OB = 2 x 1,1 = 2,2cm
- Vậy S của hình thoi trên = 1/2 x BC x AC = 1/2 x 7,68 x 2,2 = 8,45 cm2.
Tính S của hình thoi bằng cách sử dụng chiều cao và đáy.
Ngoài việc học công thức tính chu vi của hình thoi, bạn cũng cần học cách tính S của hình thoi này. Nếu bạn tính S của hình thoi theo chiều cao và đáy của hình này, chúng ta có công thức:
S = hxa
Xem thêm : ViewSonic ra mắt màn hình 4K 27 inch mới với độ sáng 400 nits, giá từ 5 triệu đồng
Trong đó:
- S: Diện tích hình thoi
- h: Chiều cao của hình thoi
- a: Cạnh dưới

Hình minh họa:
Cho hình thoi ABCD có cạnh AB = CD = BC = DA = 5cm và chiều cao của hình thoi là 4cm. Vậy hãy tính S của hình thoi này?
Trả lời:
Theo công thức tính S của hình thoi trên, ta có a = 5cm, h = 4cm và ta có:
S = a = 5,4 = 20cm2
Bài tập áp dụng công thức tính chu vi hình thoi
Để giúp bạn củng cố kiến thức về chu vi hình thoi, vui lòng xem các bài tập sau:
Bài học 1
Tính P của hình thoi khi biết hướng của các cạnh là:
Trả lời:
- P của hình thoi có cạnh là 9cm = 9 x 4 = 36cm
- P của hình thoi có cạnh là 20dm = 20 x 4 = 80dm
- P của hình thoi có cạnh là 3/4 m = 3/4 x 4 = 4m
- P của hình thoi có cạnh là 5,6cm = 5,6 x 4 = 22,4cm.
Bài 2
Tính P của hình thoi có cạnh dài 10dm?
Trả lời: P của hình thoi là: 10 x 4 = 40dm.
bài học 3
Tính P của hình thoi ABCD có cạnh bằng 7cm
Trả lời: P của hình thoi trên là: 4 x 7 = 28cm.
Bài 4
Tính độ dài tất cả các cạnh của hình thoi ABCD? Cho biết P của hình thoi này là 60cm.
Trả lời:
Gọi độ dài tất cả các cạnh của hình thoi trên là a.
P của hình thoi ABCD là 4x = 60cm
Vậy độ dài một cạnh của hình thoi trên là 60 : 4 = 15cm.

Bài 5
Tính chu vi hình thoi khi biết độ dài hai đường chéo là 30cm và 16cm?
Trả lời:
Gọi các cạnh của hình thoi trên là a và các đường chéo là d1, d2.
Chúng ta sử dụng định lý Pythagore cho tam giác vuông và thu được:
a^2 = (d1:2)^2 + (d2:2)^2 = 8^2 + 15^2.
Vậy cạnh a trong hình thoi là 17.
Vậy P của hình thoi trên = 4 x 17 = 68.
Bài 6
Cho hình thoi có tên là ABCD và biết cạnh AB bằng 15cm. Vậy hãy tính P của hình thoi này?
Trả lời: P của hình thoi trên = 15 x 4 = 60cm.
Bài 7
Tính P của hình thoi có độ dài cạnh bằng 5/6 dm?
Trả lời: P của hình thoi trên = 5/6 x 4 = 10/3dm
Bài 8
Tính độ dài các cạnh của hình thoi có P = 20cm?
Trả lời: Độ dài cạnh bên trong hình thoi này là: 20/4 = 5cm
Bài 9
Xem thêm : Đồng hồ Halei của nước nào? Có tốt không? Có nên mua không?
Cho hình thoi ABCD có P bằng 60cm. Tính độ dài tất cả các cạnh của hình này?
Trả lời:
Ta gọi a là độ dài của tất cả các cạnh bên trong hình thoi. Hãy áp dụng công thức được sử dụng để tính P của hình thoi:
P = 4 x = 60cm
Vậy độ dài một cạnh của hình thoi này là = 60/4 = 15cm

Bài 10
Cho một sân hình thoi và kéo dài hai cạnh trên về bên phải khoảng 3m, đồng thời kéo dài hai cạnh dưới khoảng 10m và biến nó thành hình bình hành có P = 106m. Tính các cạnh của sân ban đầu?
Trả lời:
Ta coi a là độ dài cạnh trong của hình thoi. Dựa vào công thức tính P của hình bình hành, ta có: P (yard) = (a+b). 2= ((a+3) + (a+10)). 2 = 106
Do đó, ta thu được kết quả của phương trình trên là độ dài cạnh của sân ban đầu là 22,5cm.
Bài tập áp dụng công thức tính diện tích hình thoi
Bên cạnh bài tập tính chu vi hình thoi, bạn cần học thêm một số bài tập giúp bạn hiểu rõ hơn về cách tính diện tích hình thoi:
Bài học 1
Cho một thửa đất hình thoi và hai đường chéo của thửa đất có tổng chiều dài là 400cm. Trong đó độ dài đường chéo thứ nhất sẽ bằng 3/5 độ dài đường chéo thứ hai. Tính S của thửa đất này?
Trả lời:
Số phần chia từ hai đường chéo của mảnh đất là 3 + 5 = 8 phần.
Chiều dài đường chéo 2 = (400/8) x 5 = 250cm
Độ dài đường chéo đầu tiên = 400 – 250 = 150cm
S của hình thoi = (250,150)/2 = 18750 cm2
Bài 2
Cho một thửa đất hình thoi có độ dài đường chéo 1 bằng 20m, độ dài đường chéo 2 bằng 3/4 độ dài đường chéo 1. Một người nông dân trồng khoai lang trên thửa đất đó và mỗi mét vuông sẽ cho thu được khoảng 5kg khoai lang. Vậy người nông dân này thu được bao nhiêu kg khoai lang?
Trả lời:
Chiều dài đường chéo 2 = (20/4) x 3 = 15m
S của mảnh đất hình thoi = (20 x 15)/2 = 150 m2
Số kilôgam khoai lang thu hoạch được trên đất = 150 x 5 = 750kg
bài học 3
Cho hình thoi ABCD có điểm O là giao điểm của 2 đường chéo. Cho S của hình thoi này là 60cm2 và cạnh AC là 10cm. Vậy hãy tính độ dài cạnh của hình thoi này?

Trả lời:
S của hình thoi = 1/2 x AC x BD
Từ đó ta suy ra được BD = (2.S) : AC = (2.60) : 10 = 12cm
Dựa vào tính chất của hình thoi, O được coi là trung điểm của các cạnh BD và AC.
Vậy cạnh OA = 1/2 x AC = 1/2 x 10 = 5cm
→ Cạnh OB = 1/2 x BD = 1/2 x 12 = 6cm
Chúng ta tiếp tục sử dụng định lý Pythagoras trong tam giác có tên AOB và thu được:
AB^2 = OA^2 + OB^2 = 5^2 + 6^2 = 61 → Cạnh AB dài 7,81cm (là độ dài các cạnh của hình thoi ABCD ở trên)
Như vậy, bài viết đã cung cấp kiến thức về chu vi và diện tích hình thoi cho mọi người cùng học. Đặc biệt, học sinh phải nắm vững công thức này và giải các bài tập liên quan thường xuyên để làm bài thi tốt hơn. Hiện nay, tất cả các dạng bài tập hình học đều đề cập đến hình thoi và công thức của chúng.
Xem các bài viết liên quan:
Nguồn: https://tuyengiaothudo.vn
Danh mục: Khám phá