Hiện nay có rất nhiều bạn học sinh chưa biết cách tính diện tích hình quạt tròn vì chưa hiểu rõ công thức của nó. Đây chính là kiến thức giúp các bạn học tốt môn hình học trên lớp. Chính vì vậy, trong bài viết dưới đây, chúng tôi sẽ chia sẻ công thức tính diện tích hình quạt tròn để các bạn học tập và áp dụng vào các dạng bài tập thường gặp hiện nay.
Công thức tính diện tích hình tròn là gì?
Trước khi tìm hiểu công thức tính diện tích hình quạt tròn, chúng ta phải tìm hiểu về hình tròn và cách tính diện tích của hình này. Diện tích hình tròn (S) thường là phần nằm bên trong hình tròn. Việc tìm hiểu cách tính S của hình tròn có nguồn gốc từ thời cổ đại và được người Hy Lạp nghiên cứu trước Công nguyên.
Bạn đang xem: Công thức tính diện tích hình quạt tròn

Các nhà toán học Hy Lạp nhận ra rằng S của một vòng tròn liên quan đến độ dài của bán kính bình phương. Nghĩa là, một khi mọi người biết độ dài của bán kính trong một vòng tròn, họ có thể tính S của nó bằng cách sử dụng công thức như thế này:
S = π x R^2 (đơn vị đo diện tích)
Công thức tính diện tích hình quạt là gì?
Khi bạn đã học cách tính S của một đường tròn, bạn sẽ thấy rằng nó liên quan đến một hình quạt tròn thông qua thông tin sau:
Quạt tròn là gì?
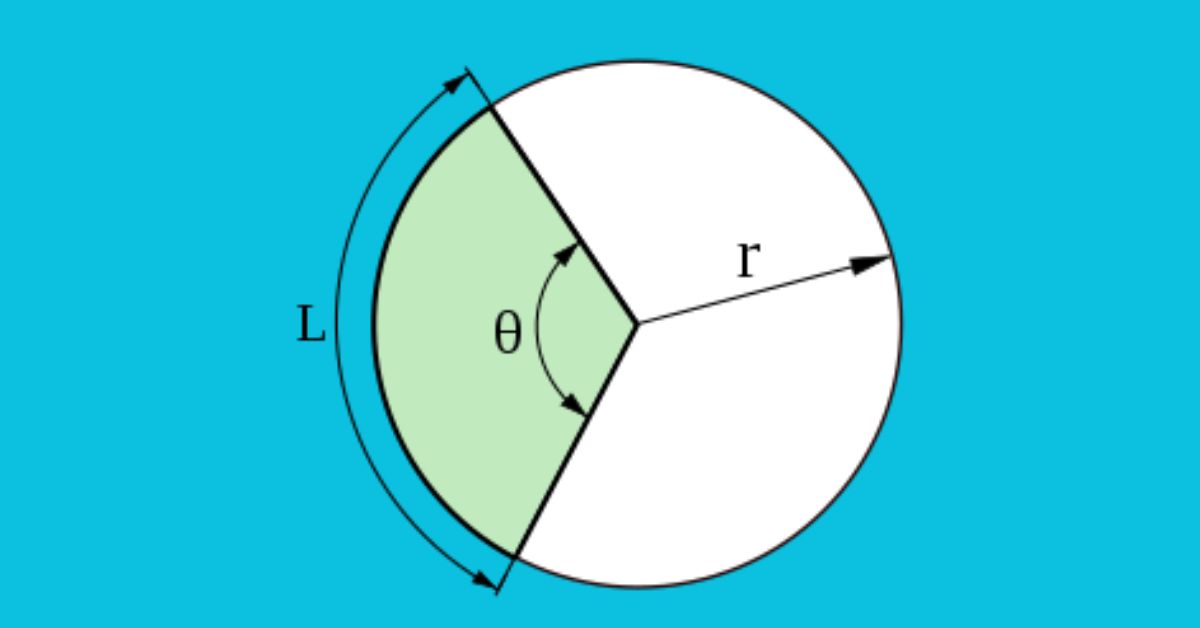
Diện tích (S) của một hình quạt là một định nghĩa khá quan trọng trong toán học và hình học. Để hiểu rõ hơn về diện tích của hình này, hãy nghĩ đến một hình tròn trên mặt phẳng. Bên trong hình tròn này có một tâm và một đường viền. Để tạo ra một hình quạt tròn, bạn chỉ cần chọn 2 điểm ngẫu nhiên ở đường viền bên trong và nối nó với tâm của hình tròn.
Công thức được sử dụng để tính toán hình dạng quạt chữ S
Do đó, S của đường tròn tạo bởi hai tia trên là S của một cung tròn. Để tính S này, hãy sử dụng góc giữa hai tia bắt đầu và kết thúc. Góc tạo ra sẽ được đo bằng độ và đây là yếu tố quyết định cho S của cung tròn. Điểm quan trọng nhất là S của cung tròn là một phần của S của một đường tròn hoàn hảo và chứa hai tia tạo thành cung tròn.
Để tính S của quạt, ta cần lấy tỉ số góc tạo bởi hai tia và nhân với tổng diện tích hình tròn. Công thức tính diện tích quạt hiện nay được áp dụng trong nhiều lĩnh vực trong thực tế, từ địa lý, khoa học tự nhiên đến kỹ thuật. Sau đây là công thức cụ thể để tính S của quạt có bán kính R:

Bao gồm:
- l là độ dài cung n° của hình quạt.
- n°: số đo độ cung
- π: hằng số xấp xỉ 3,14
- R: bán kính hình tròn.
Tổng hợp các bài tập trắc nghiệm về diện tích hình quạt
Để áp dụng kiến thức về cách tính S của hình quạt ở trên, vui lòng làm theo các bài tập trắc nghiệm sau:
Bài tập 1: Một hình tròn có S bằng 225π cm2. Vậy độ dài R của hình tròn này là bao nhiêu?
- A. 15cm
- B. 16cm
- C. 12cm
- D. 14 cm
Trả lời:
Ta có S = R^2 x π = 225. Do đó R^2 = 225 và do đó chiều dài R là 15cm.
Bài 2: Tính diện tích hình tròn có bán kính R = 10cm?
- A. 100π cm²
- B. 10π cm²
- C. 20π cm²
- D. 100π² cm²
Trả lời:
S = π X r^2 = 100π (cm2)

Bài tập 3: Cho đường tròn tâm O, bán kính 10cm, đường kính AB. Lấy điểm M trên đường tròn tâm O sao cho góc BAM bằng 45 độ. Tính S của hình quạt tròn AOM.
- A. 5π (cm²)
- B. 25π (cm²)
- C. 50π (cm²)
- D. 25/2π (cm²)
Trả lời:
Chúng ta có một đường tròn tâm O và bán kính 10cm:
- OA = OM
- Góc MOA là 45 độ
Do đó tam giác AMO là tam giác vuông và góc MOA bằng 90 độ.
Sau đó, chúng ta có thể tính S của hình quạt có tên AOM như sau:
S = (π x R² xn°)/360
= (π x 10^2 x 90)/360
= 25π (cm²)
Tuyển tập bài tập tính diện tích hình quạt tròn
Ngoài các bài tập trắc nghiệm đơn giản trên, bạn có thể tham khảo thêm một số bài tập tự luận về cách tính diện tích hình quạt như sau:
Bài học 1
Cho đường tròn tâm O, đường kính AB, độ dài 3√3. Cho điểm C trên đường tròn và tạo một góc ABC bằng 60 độ. Tính S của đoạn BC (Diện tích đường tròn giới hạn bởi 1 cung tròn và 1 dây cung).

Trả lời:
Xét một đường tròn có tâm O và góc ACB bằng 90 độ.
Do đó, góc CAB = 90 độ – góc CBA = 60 độ (Tam giác ABC vuông tại C)
Xem thêm : Công thức tính thể tích khối tròn xoay và ví dụ minh họa
Góc BOC và góc CAB là hai góc nội tiếp và là hai góc ở tâm chắn cung.
Do đó, góc BOC lớn gấp đôi góc CAB = 2 x 30 độ = 60 độ.
Vì vậy, hình quạt S có tên là AOC là: S = (π x R^2 x 60)/360 = π x R^2/6
Chúng ta tiếp tục xét tam giác có tên AOC và thu được:
- Góc BOC bằng 60 độ
- OC = OA = R
Do đó, tam giác đều BOC có các cạnh R.
Ta gọi đường cao của tam giác AOC là H và ta có:
CH = CO x sin của góc 60 độ = √3R/2
Do đó S của tam giác AOC = 1/2 x CH x OA = √3R^2/4
Như vậy, S của đoạn thẳng BC sẽ bằng diện tích hình quạt AOC – S của tam giác BOC:
⇔ π x R^2/6 – √3R^2/4 = (18π – 27√3)/16 (cm²)
Bài 2
Tính toán và điền kết quả vào bảng như sau:
| R của đường tròn | Chiều dài của hình tròn | Vòng tròn S | Đo vòng cung | Hình quạt chữ S |
| 12cm | 45 độ | |||
| 2cm | 10,5cm2 | |||
| 40cm2 | 10cm2 |
Trả lời:
Ta có chiều dài của hình tròn = 12cm nên ta có thể suy ra C là 12cm. Khi đó R của hình tròn là: R = C/ 2π = 12/2π = 1,91cm.
Vậy S của hình tròn có R = 1,91cm là: S = R^2 x π = 1,91^2 x π = 11,46 cm2.
Do đó, S của một hình quạt 45 độ là: S’ = (π x R^2 xn)/360 = (π x 1,91^2 x 45)/ 360 = 1,43cm2.
Vì bán kính hình tròn là 2cm nên ta có chiều dài hình tròn = C = 2πxR = 2π x R = 2π x 2 = 12,57cm.
Vì vậy, S của đường tròn được tính là S = R^2 x π = 2^2 x π = 12,57cm2.
Vì diện tích của hình quạt = 10,5cm2 nên số đo của cung tròn là n = (360 x S’)/ (π x R^2) = (360 x 10,5)/ 12,57 = 300 độ.
Vì S của đường tròn là 40cm2 nên ta có thể suy ra R của đường tròn là R = √S/R = √40/π = 3,57cm.
Vậy ta có chu vi của cung tròn là C = 2π x R = 2π x 3,57 = 22,42cm.
Vì ta có S của hình quạt = 1/4 S của hình tròn, nên ta có số đo của cung bằng 90 độ.
Vì vậy, chúng ta sẽ điền vào bảng trên với các kết quả sau:
| R của đường tròn | Chiều dài của hình tròn | Vòng tròn S | Đo vòng cung | Khu vực dành cho người hâm mộ |
| 1,91cm | 12cm | 11,46cm2 | 45 độ | 1,43cm2 |
| 2cm | 12,57cm | 12,57cm2 | 300 độ | 10,5cm2 |
| 3,57cm | 22,42cm | 40cm2 | 90 độ | 10cm2 |
bài học 3
Cho một hình vuông có cạnh dài 5cm và nội tiếp đường tròn tâm O. Hãy tính độ dài đường tròn tâm O và tính S của đường tròn này?

Trả lời:
Gọi hình vuông trên là ABCD, ta có:
OD = OC = OB = OA = R. Do đó, điểm O là giao điểm của đoạn thẳng AC với đoạn thẳng BD. Từ đó, ta có thể suy ra rằng R = AC/2
Xét tam giác ABC vuông tại B, ta có:
AC^2 = AB^2 + BC^2 (Pythagoras)
AC^2 = 5^2 + 5^2
AC^2 = 25 + 25
AC^2 = 50
→ AC = 5√2 cm
Xem thêm : Top 5 bản mở rộng hay nhất trong The Sims 4 mà bạn không thể bỏ lỡ
Vậy ta có R của đường tròn bằng R = AC/2 = (5√2)/2 (cm)
Vậy ta có C của đường tròn bằng: 2π x R = 2 x π x ((5√2)/2)) (cm)
Vì vậy, chúng ta có S của đường tròn này bằng: S = π x R^2 = π x ((5√2)/2)^2 = (25/2)π (cm^2)
Bài 4
Cho đường tròn tâm O bán kính R và một điểm M sao cho OM = 2R. Từ điểm M, kẻ các tiếp tuyến như MA, MB với các điểm A và B là các điểm tiếp xúc.
- Tính độ dài cung AB.
- Tính S giới hạn bởi 2 tiếp tuyến BM và AM với cung AB.

Trả lời:
a. Vì đoạn thẳng AM là tiếp tuyến của đường tròn tâm O nên đoạn thẳng AM vuông góc với đoạn thẳng OA.
Xét tam giác có tên OAM vuông tại A, ta có:
cos của góc AOM = OA/OM = R/2R = 1/2
Do đó, góc AOM bằng 60 độ. Và đoạn thẳng OM cũng là tia phân giác của góc AOB (2 tiếp tuyến khi cắt nhau).
Vậy góc AOB = 120 độ
Vậy độ dài cung AB = l = 9π x R x 120)/180 = (2π x R)/3 cm
b. Xét tam giác có tên OAM và có góc vuông tại A:
AM^2 + AO^2 = OM^2 (Pythagore)
→ AM^2 + R^2 = (2R)^2
→ AM^2 = 4 x R^2 – R^2
→ AM = √3x R
Vậy S của tam giác có tên OAM sẽ bằng:
S = 1/2 AM x AO = 1/2 x R x √3R = (√3 x R^2)/2
Xét hai tam giác AOM và BOM, ta có:
- OM là đoạn chung
- BO = AO = R
- AM = BM (các tiếp tuyến có thể cắt nhau)
Do đó, tam giác AOM bằng tam giác BOM (cạnh – cạnh – cạnh)
Do đó, diện tích tam giác AOM = Diện tích tam giác BOM = (√3 x R^2)/2
Do đó, diện tích của AMBO = Diện tích của AOM + Diện tích của BOM =
(√3 x R^2)/2 + (√3 x R^2)/2 = √3 x R^2
Vậy diện tích hình quạt tròn có cung AB là: S = (π x R^2 x 120 độ)/ 360 = (π x R^2)/3
Diện tích phần đất giới hạn bởi các tiếp tuyến MB, MA và cung AB là:
S = Diện tích AMBO + Diện tích hình quạt tròn có cung AB = √3 x R^2 + (π x R^2)/3 = R^2 x (√3 – (π/3))
Một số bài toán tự luyện về tính diện tích hình quạt
Bạn có thể thực hành thêm một vài bài tập về công thức tính S của hình quạt sau:
Bài tập 1: Cho hình quạt có C = 28cm và S = 49cm2. Tính R của hình quạt này.
Bài tập 2: Cho đường tròn tâm I, bán kính 2cm. Vẽ các đường thẳng bán kính IB, IA sao cho góc AIB bằng 120 độ. Tính:
- Tính độ dài cung AB.
- Tính S của hình quạt giới hạn bởi cung AB có 2 bán kính IB và IA.

Bài tập 3: Cho 2 đường tròn cùng tâm O. Bán kính của 2 đường tròn này là r = 5cm và r = 2cm. Lấy hai điểm A và B sao cho chúng thuộc đường tròn O và đảm bảo rằng góc AOB bằng 70 độ. Các tia OB, OA cắt đường tròn có tâm O và bán kính R tại các điểm D, E. Lấy điểm C bên trong đường tròn O.
- Tính số đo của góc DCE và góc DOE.
- Tính độ dài đường tròn tâm O bán kính R và tính độ dài đường tròn tâm O bán kính r bằng cung DE.
- Tính S của đường tròn tâm O, bán kính r và tính DOE của hình quạt.
Nội dung trên đã chia sẻ kiến thức về công thức tính diện tích hình quạt tròn và các bài tập liên quan. Học sinh cần nắm vững kiến thức này để làm bài kiểm tra hình học tốt hơn.
Xem các bài viết liên quan:
Nguồn: https://tuyengiaothudo.vn
Danh mục: Khám phá