Cách tính thể tích khối lăng trụ và ví dụ minh hoạ

Thể tích của lăng trụ là một trong những bài tập hình học không gian thú vị. Biết cách tính thể tích của lăng trụ giúp học sinh giải các bài tập trên lớp và vận dụng vào thực tế. Vậy cách tính thể tích của lăng trụ như thế nào? Hãy cùng theo dõi bài viết dưới đây của tuyengiaothudo.vn để biết thông tin chi tiết nhé!

Có thể bạn quan tâm

Định nghĩa

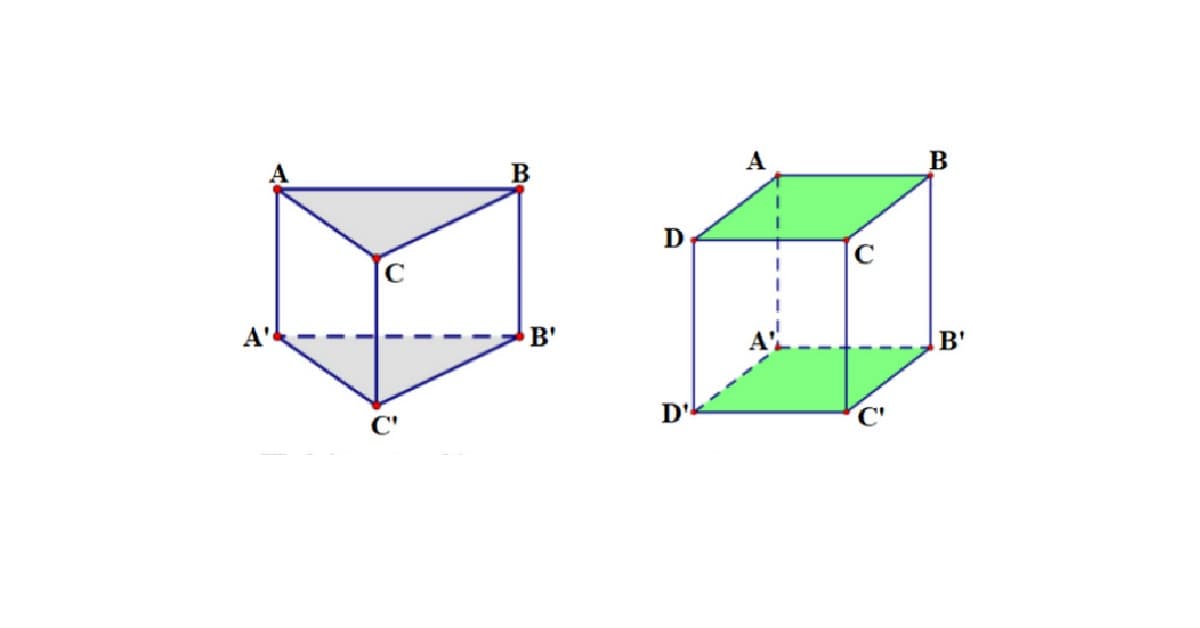
Lăng trụ hay còn gọi là lăng trụ là một hình dạng phổ biến trong cuộc sống. Lăng trụ được chia thành lăng trụ đứng, lăng trụ đều, lăng trụ tam giác đều và một số hình dạng đặc biệt khác. Dưới đây, chúng tôi sẽ tóm tắt định nghĩa và tính chất của từng hình dạng để bạn hiểu rõ:

Bạn đang xem: Cách tính thể tích khối lăng trụ và ví dụ minh hoạ

Lăng kính

Lăng trụ là khối đa diện gồm hai đáy nằm trên hai mặt phẳng và song song với nhau, là hai đa giác bằng nhau. Theo đó, đáy của lăng trụ có thể là hình chữ nhật, hình vuông, hình bình hành, hình tam giác, v.v. Các mặt bên của lăng trụ sẽ là các hình bình hành, có các cạnh bằng nhau và song song.

Sau khi học xong định nghĩa, bạn cần hiểu được tính chất của lăng trụ để vận dụng linh hoạt vào giải bài tập. Tính chất của lăng trụ bao gồm:

Hai đáy của lăng trụ là hai đa giác bằng nhau nằm trên hai mặt phẳng song song.
Các cạnh bên của lăng trụ song song với nhau.
Các mặt bên của lăng trụ là hình bình hành.

Lăng kính phải

Khi nghiên cứu thể tích của một lăng trụ, chúng ta đang tính thể tích của một lăng trụ đứng. Định nghĩa của lăng trụ đứng là một hình có hai cạnh đáy là hai đa giác phẳng, bằng nhau và nằm trên hai mặt phẳng song song. Một lăng trụ đứng sẽ có các mặt bên hình chữ nhật, vuông góc với các mặt phẳng đáy đa giác. Chiều cao của lăng trụ đứng là chiều dài của mặt bên. Dựa trên đa giác đáy của lăng trụ đứng, chúng ta đặt tên cho nó, chẳng hạn như lăng trụ đứng tứ giác, lăng trụ đứng tam giác, v.v.

Các tính chất của lăng trụ đứng bao gồm:

Lăng trụ đứng có các cạnh bên vuông góc với đáy.
Lăng trụ đứng có các mặt bên là hình chữ nhật.
Các mặt phẳng chứa đáy lăng trụ thì song song với nhau.
Độ dài cạnh của lăng trụ đứng là chiều cao.

Lăng kính đều

Định nghĩa về lăng trụ đều, còn gọi là lăng trụ vuông, có đáy là đa giác đều. Khi nghiên cứu về thể tích của lăng trụ, hẳn bạn đã từng nghe đến lăng trụ tam giác đều, lăng trụ tứ giác đều, v.v. Vì đáy của lăng trụ là đa giác đều nên các cạnh đáy sẽ bằng nhau. Ngoài ra, các cạnh bên của lăng trụ là hình chữ nhật và sẽ vuông góc với đáy.

Các công thức liên quan đến lăng kính

Tương tự như một số hình học không gian khác, lăng trụ bao gồm các công thức để tính diện tích xung quanh, diện tích toàn phần và thể tích của lăng trụ. Chúng tôi sẽ chia sẻ từng công thức trong phần bên dưới để bạn theo dõi!

Tính diện tích bên

Diện tích xung quanh của lăng trụ đứng bằng tổng diện tích các mặt bên hoặc có thể nhân chu vi đáy với chiều cao. Sxq = ph (P là chu vi đáy và h là chiều cao)

Nhìn chung, cách tính diện tích xung quanh của lăng trụ đứng khá đơn giản. Tuy nhiên, để giúp bạn hiểu rõ hơn về công thức này, chúng ta sẽ lấy một ví dụ cụ thể. Cho lăng trụ đứng tam giác ADCDEF. Tính diện tích xung quanh của lăng trụ đứng trên?

Giải: Dựa vào dữ kiện đã cho, ta biết từng cạnh đáy để tính chu vi và chiều cao. Lưu ý, bài toán yêu cầu tính diện tích xung quanh chứ không phải thể tích của lăng trụ, nên ta cần áp dụng đúng công thức. Sxq = (3+4+5) x 7 = 84 (cm2) Như vậy ta tìm được diện tích xung quanh của lăng trụ ABCDEF là 84cm.

Tổng diện tích của lăng trụ

Tổng diện tích của một lăng trụ được tính bằng cách cộng diện tích xung quanh với diện tích của hai đáy. Do đó, để tính tổng diện tích, chúng ta phải tính diện tích xung quanh. Stp = Sxq + S2Base

Chúng ta sẽ tiếp tục lấy ví dụ trong lăng trụ ABCDEF ở trên, để tính diện tích toàn phần, chúng ta cần tính diện tích đáy. Đây là lăng trụ tam giác nên diện tích đáy là 1/2 x 3 x 4 = 6 (cm2). Sau khi biết diện tích xung quanh, diện tích đáy sẽ tính được diện tích toàn phần.

Stp = 84 + 2 x 6 = 96 (cm2) => Vậy diện tích toàn phần của lăng trụ đứng ABCDEF là 96 cm2.

Thể tích của lăng kính

Xem thêm : Số 11 có may mắn không? Giải mã con số 11 có ý nghĩa gì?

Thể tích của lăng trụ được áp dụng trong thực tế. Thể tích của lăng trụ đứng được tính bằng cách nhân diện tích đáy với chiều cao. V = Diện tích đáy x chiều cao

Ví dụ: Cho một lăng trụ đứng có đáy là hình chữ nhật có chiều rộng 3cm, chiều dài 4cm và chiều cao 5,5cm. Tính thể tích của lăng trụ với các thông số đã cho.

Giải pháp: Theo dữ liệu ban đầu, xác định rằng đây là một lăng trụ chữ nhật. Đầu tiên, chúng ta sẽ tính diện tích đáy Sbase = 3 x 4 = 12 (cm2). Tiếp theo, chúng ta tính thể tích của lăng trụ bằng V = 12. 5,5 = 66 (cm2). Như vậy, chúng ta đã tính được thể tích của lăng trụ cần tìm là 66 cm2.

Một số hình dạng lăng kính đặc biệt

Ngoài lăng trụ đã nêu ở trên, trong hình học không gian còn có một số lăng trụ đặc biệt như hộp đứng, hộp chữ nhật, khối lập phương. Để mở rộng kiến thức về lăng trụ, chúng tôi sẽ chia sẻ định nghĩa và tính chất của một số lăng trụ đặc biệt để bạn tham khảo:

Hộp dọc

Một hộp có các cạnh vuông góc với đáy được gọi là hộp đứng. Theo đó, một hộp đứng sẽ có đáy là hình bình hành và các mặt xung quanh sẽ là hình chữ nhật.

Hình hộp chữ nhật

Một hộp có đáy hình chữ nhật được gọi là hộp chữ nhật. Do đó, một hộp chữ nhật sẽ có tất cả 6 mặt bao quanh là hình chữ nhật. Ngoài ra, lăng trụ đặc biệt này sẽ có tổng cộng 12 cạnh, 8 đỉnh và 6 mặt. Hai đỉnh đối diện của một hộp chữ nhật là đường chéo có hai đầu và đồng quy tại một điểm. Diện tích và chu vi của các mặt đối diện của một hộp chữ nhật được xác định là bằng nhau.

Hình khối

Hình lập phương là một lăng trụ đặc biệt, là một lăng trụ chữ nhật có hai đáy và bốn mặt bên đều là hình vuông. Đây là một khối đa diện có các mặt vuông và mỗi đỉnh là một đỉnh chung của ba mặt.

Một số bài tập về lăng kính

Như vậy, chúng tôi đã tóm tắt kiến thức lý thuyết, cách tính diện tích xung quanh, diện tích toàn phần, thể tích của lăng trụ để các bạn nắm bắt. Để giải các bài tập liên quan đến lăng trụ, các bạn cần luyện tập chăm chỉ. Dưới đây, chúng tôi sẽ cung cấp một số bài tập thường gặp có kèm lời giải để các bạn tham khảo:

Bài học 1

Cho một lăng trụ có kích thước như hình dưới đây, lưu ý rằng đáy của lăng trụ là một tam giác vuông. Tính diện tích xung quanh và thể tích của lăng trụ này?

Làm:

Đầu tiên, ta cần tính chu vi đáy của lăng trụ. Theo hình vẽ, chu vi của tam giác ABC là 12cm, chiều cao là 6cm. Tiếp theo, ta sẽ tính diện tích xung quanh của lăng trụ ABCDEF = 12 x 6 = 72cm2.

Ta có diện tích đáy của lăng trụ bằng 6cm2 => thể tích của lăng trụ ABCDEF = S xh = 6 x 6 = 36cm3. Như vậy, ta đã tính được diện tích xung quanh của lăng trụ bằng 72cm2 và thể tích bằng 36cm3.

Bài 2

Cho một lăng trụ đứng có đáy là hình chữ nhật, hãy tính diện tích xung quanh và thể tích của hình đó?

Làm:

Tương tự như trên, trước tiên ta cần tính chu vi đáy = 2.(1+ 3) = 8 và chiều cao là 5cm.

Diện tích hình lăng trụ đứng = C xh = 8 x 5 = 40cm2.

Để tính thể tích của lăng trụ, trước tiên hãy tính diện tích đáy = 3 x 1 = 3cm2

Thể tích của lăng trụ đứng = S xh = 3 x 5 = 15cm3.

bài học 3

Dựa vào hình lăng trụ sau, hãy xác định số cạnh.

9 mặt
8 mặt
5 mặt
6 mặt

Trả lời: Về lý thuyết, đây là một lăng trụ tam giác có 6 đỉnh, 5 mặt và 9 cạnh => đáp án đúng là A. 9 cạnh. Đây là một câu hỏi lý thuyết thường gặp trong bài kiểm tra, vì vậy bạn cần nắm chắc kiến thức nhé!

Bài 4

Cho hình lăng trụ tứ giác bên dưới có kích thước chi tiết. Tính thể tích của hình lăng trụ và chọn câu trả lời đúng?

V = 80 cm3
V = 18 cm3
V = 19 cm3
V = 90 cm3

Làm:

Bài trắc nghiệm về thể tích của lăng trụ cũng rất phổ biến trong các bài kiểm tra. Theo lăng trụ trên, ta có thể xác định được đáy là hình thang đều => diện tích đáy = 12.(4+8).3=18 => S=12.(4+8).3=18 (cm2)

Sau khi tính diện tích một đáy, thể tích của lăng trụ có thể tính được là V = 18,5 = 90 (cm3). Vậy đáp án đúng của câu hỏi này là D.

Bài 5

Tiếp theo là một dạng bài tập về lăng trụ, yêu cầu bạn tính diện tích xung quanh và sau đó khoanh tròn câu trả lời đúng.

7 200 cm2
6 900 cm2
6 250 cm2
7 900 cm2

Làm:

Xác định rằng đây là lăng trụ tam giác nên diện tích xung quanh = 45 + 20 + 50). 60 = 6 900 (cm2). Do đó, B là câu trả lời đúng cho bài tập này.

Phần kết luận

Trong bài viết trên chúng tôi đã chia sẻ cách tính thể tích hình lăng trụ để các bạn tham khảo. Ngoài ra chúng tôi cũng hướng dẫn các bạn giải một số bài tập thường gặp. Hy vọng các bạn sẽ nắm vững kiến thức lý thuyết và có đủ kỹ năng để giải các bài tập liên quan. Hãy click theo dõi fanpage tuyengiaothudo.vn và kênh Youtube Kênh Hoàng Hà để bạn không bỏ lỡ bất kỳ thông tin thú vị nào từ chúng tôi!

XEM THÊM:

Nguồn: https://tuyengiaothudo.vn
Danh mục: Khám phá